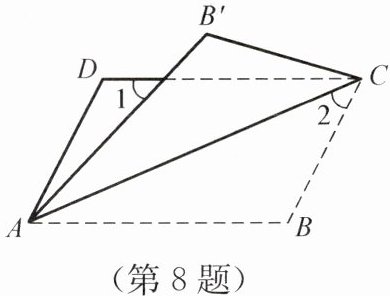
8. 如图所示,将$□ ABCD沿对角线AC$折叠,使点$B落在点B'$处,若$∠1= ∠2= 44^{\circ}$,则$∠B$为(
A.$66^{\circ}$
B.$104^{\circ}$
C.$114^{\circ}$
D.$124^{\circ}$
C
)
A.$66^{\circ}$
B.$104^{\circ}$
C.$114^{\circ}$
D.$124^{\circ}$
答案:
C
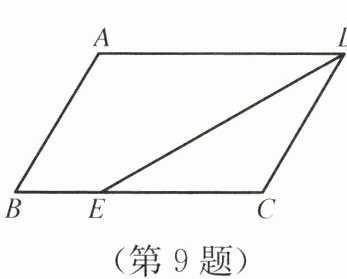
9. 如图所示,在$□ ABCD$中,$DE平分∠ADC$,$AD= 6$,$BE= 2$,则$□ ABCD$的周长是
20
。
答案:
20
10. 如图所示,在菱形$ABCD$中,点$M$、$N分别在AB$、$CD$上,且$AM= CN$,$MN与AC交于点O$,连接$BO$。若$∠DAC= 28^{\circ}$,则$∠OBC$的度数为
62°
。
答案:
62°
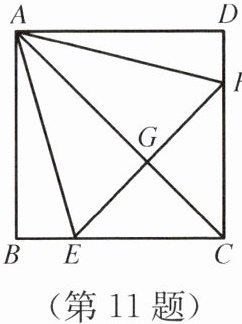
11. 如图所示,正方形$ABCD$中,点$E$、$F分别在BC$、$CD$上,$\triangle AEF$是等边三角形,连接$AC交EF于点G$,下列结论:①$BE= DF$;②$∠DAF= 15^{\circ}$;③$AC垂直平分EF$;④$BE+DF= EF$。其中正确结论是____(填序号)。

①②③
答案:
①②③
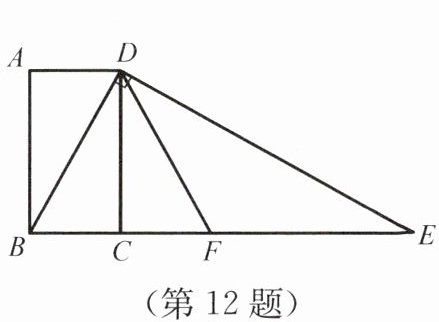
12. 如图所示,四边形$ABCD$为矩形,过点$D作对角线BD$的垂线,交$BC的延长线于点E$,取$BE的中点F$,连接$DF$,$DF= 4$。设$AB= x$,$AD= y$,则$x^{2}+(y-4)^{2}$的值为____
16
。
答案:
16 提示:在Rt△BDE中,点F平分BE,所以BF= $\frac{1}{2}$BE=DF=4.因为四边形ABCD是矩形,所以CD=AB=x,BC=AD=y.在Rt△DCF中,CD²+CF²=DF²,所以x²+(4 - y)²=4²=16.
13. 在菱形$ABCD$中,$∠A= 30^{\circ}$,在同一平面内,以对角线$BD为底边作顶角为120^{\circ}的等腰三角形BDE$,则$∠EBC$的度数为
45°或105°
。
答案:
45°或105°
14. 如图所示,在平行四边形$ABCD$中,$∠A= 70^{\circ}$,将平行四边形折叠,使点$D$、$C分别落在点F$、$E$处(点$F$、$E都在AB$所在的直线上),折痕为$MN$,则$∠AMF= $
40°
。
答案:
40°
15. 如图所示,在一张矩形纸片$ABCD$中,$AD= 2cm$,$E$、$F分别是CD$、$AB$的中点,现将这张纸片折叠,使点$B落在EF上的点G$处,折痕为$AH$,若$HG的延长线恰好经过点D$,则$CD$的长为
$\sqrt{3}$
cm。
答案:
$\sqrt{3}$ cm
查看更多完整答案,请扫码查看


