《2025年暑假生活江苏人民出版社八年级数学》

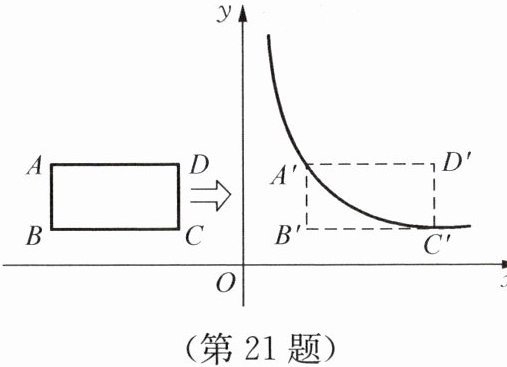
21. 如图所示,已知在平面直角坐标系中,四边形$ABCD$是矩形,$AD// x$轴,点$A的坐标为(-3,\frac {3}{2})$,$AB= 1$,$AD= 2$。
(1)直接写出$B$、$C$、$D$三点的坐标；
(2)将矩形$ABCD向右平移m$个单位长度,使点$A$、$C恰好同时落在反比例函数y= \frac {k}{x}(x＞0)$的图像上,得矩形$A'B'C'D'$,求矩形$ABCD的平移距离m$和反比例函数的关系式。

答案：
(1) $ B(-3,\frac{1}{2}) $, $ C(-1,\frac{1}{2}) $, $ D(-1,\frac{3}{2}) $;
(2) 解：由平移性质得 $ A'(-3+m,\frac{3}{2}) $, $ C'(-1+m,\frac{1}{2}) $.
∵点 $ A' $, $ C' $ 在反比例函数 $ y=\frac{k}{x} $ 图像上，
∴ $ k=(-3+m)×\frac{3}{2}=(-1+m)×\frac{1}{2} $.
解得 $ m=4 $.
∴ $ k=(-3+4)×\frac{3}{2}=\frac{3}{2} $.
故平移距离 $ m=4 $，反比例函数关系式为 $ y=\frac{3}{2x} $.

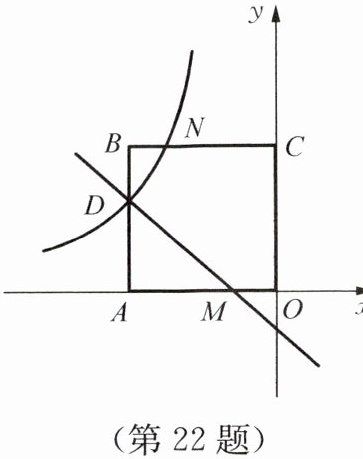
22. 如图所示,已知在平面直角坐标系中,正方形$OABC的顶点O$与坐标原点重合,点$C的坐标为(0,3)$,点$A在x$轴的负半轴上,点$D$、$M分别在边AB$、$OA$上,且$AD= 2DB$,$AM= 2MO$,一次函数$y= kx+b的图像过点D$、$M$,反比例函数$y= \frac {m}{x}的图像经过点D$,与$BC的交点为N$。
(1)求反比例函数和一次函数的表达式；
(2)若点$P在直线DM$上,且使$\triangle OPM的面积与四边形OMNC$的面积相等,求点$P$的坐标。

答案：
(1) 正方形$OABC$中，$C(0,3)$，则$OC=OA=3$，点$A(-3,0)$，$B(-3,3)$。
$AD=2DB$，$AB=3$，则$AD=2$，$D(-3,2)$。
反比例函数$y=\frac{m}{x}$过点$D$，$2=\frac{m}{-3}$，$m=-6$，反比例函数表达式为$y=-\frac{6}{x}$。
$AM=2MO$，$OA=3$，则$MO=1$，$M(-1,0)$。
一次函数$y=kx+b$过$D(-3,2)$、$M(-1,0)$，
$\begin{cases}-3k+b=2 \\ -k+b=0\end{cases}$，解得$\begin{cases}k=-1 \\ b=-1\end{cases}$，一次函数表达式为$y=-x-1$。
(2) 四边形$OMNC$中，$N$在$BC$上，$BC$：$x=0$（应为$y=3$），由$y=3$代入$y=-\frac{6}{x}$，$x=-2$，$N(-2,3)$。
$OM=1$，$OC=3$，$CN=2$，$S_{OMNC}=\frac{1}{2}×(OM+CN)× OC=\frac{1}{2}×(1+2)×3=\frac{9}{2}$。
设$P(t,-t-1)$，$\triangle OPM$面积$S=\frac{1}{2}× OM×|y_P|=\frac{1}{2}×1×|-t-1|=\frac{9}{2}$，
$|-t-1|=9$，$-t-1=9$或$-t-1=-9$，解得$t=-10$或$t=8$，
点$P$坐标为$(-10,9)$或$(8,-9)$。
(1) 反比例函数：$y=-\frac{6}{x}$，一次函数：$y=-x-1$；
(2) $P(-10,9)$或$(8,-9)$。