《2025年暑假生活江苏人民出版社八年级数学》

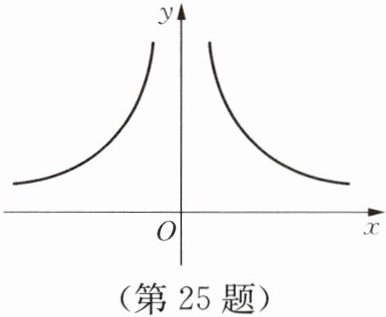
25. 如图所示,在平面直角坐标系$xOy$中,点$A$、$B分别在函数y_{1}= \frac {4}{x}(x＞0)与y_{2}= -\frac {4}{x}(x＜0)$的图像上,点$A$、$B的横坐标分别为a$、$b$。
(1)若$AB// x$轴,求$\triangle OAB$的面积；
(2)若$\triangle OAB是以AB$为底边的等腰三角形,且$a+b≠0$,求$ab$的值。

答案：
(1) 因为点$A$在$y_{1}=\frac{4}{x}(x＞0)$上，横坐标为$a$，所以$A(a,\frac{4}{a})$。点$B$在$y_{2}=-\frac{4}{x}(x＜0)$上，横坐标为$b$，所以$B(b,-\frac{4}{b})$。
由于$AB// x$轴，所以点$A$和点$B$的纵坐标相等，即$\frac{4}{a}=-\frac{4}{b}$，化简得$b=-a$。
$AB$的长度为$a - b = a - (-a) = 2a$，点$O$到$AB$的距离为点$A$的纵坐标的绝对值，即$\left|\frac{4}{a}\right|=\frac{4}{a}$（因为$a＞0$）。
所以$\triangle OAB$的面积为$\frac{1}{2}× AB×$高$=\frac{1}{2}× 2a×\frac{4}{a}=4$。
(2) 因为$\triangle OAB$是以$AB$为底边的等腰三角形，所以$OA=OB$。
$OA^{2}=a^{2}+\left(\frac{4}{a}\right)^{2}$，$OB^{2}=b^{2}+\left(-\frac{4}{b}\right)^{2}=b^{2}+\left(\frac{4}{b}\right)^{2}$。
则$a^{2}+\frac{16}{a^{2}}=b^{2}+\frac{16}{b^{2}}$，移项得$a^{2}-b^{2}+\frac{16}{a^{2}}-\frac{16}{b^{2}}=0$，因式分解得$(a^{2}-b^{2}) + 16\left(\frac{b^{2}-a^{2}}{a^{2}b^{2}}\right)=0$，即$(a^{2}-b^{2})\left(1 - \frac{16}{a^{2}b^{2}}\right)=0$。
因为$a＞0$，$b＜0$，所以$a^{2}\neq b^{2}$，则$1 - \frac{16}{a^{2}b^{2}}=0$，即$a^{2}b^{2}=16$，所以$ab=\pm4$。
又因为$a＞0$，$b＜0$，所以$ab＜0$，故$ab=-4$。
(1) $4$；
(2) $-4$