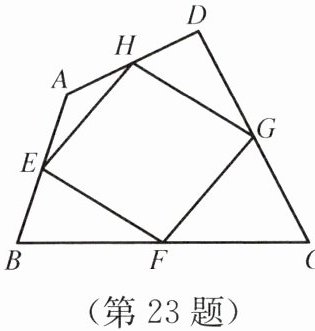
23. 如图所示,我们把依次连接任意四边形$ABCD各边中点所得四边形EFGH$叫中点四边形。
(1)若四边形$ABCD$是菱形,则它的中点四边形$EFGH$一定是____;
A. 菱形
B. 矩形
C. 正方形
D. 梯形
(2)若四边形$ABCD的面积为S_{1}$,中点四边形$EFGH的面积记为S_{2}$,则$S_{1}与S_{2}$的数量关系是____;
(3)在四边形$ABCD$中,沿中点四边形$EFGH$的其中三边剪开,可得三个小三角形,将这三个小三角形与原图中未剪开的小三角形拼接成一个平行四边形,请画出一种拼接示意图,并写出对应全等的三角形。
(1)若四边形$ABCD$是菱形,则它的中点四边形$EFGH$一定是____;
A. 菱形
B. 矩形
C. 正方形
D. 梯形
(2)若四边形$ABCD的面积为S_{1}$,中点四边形$EFGH的面积记为S_{2}$,则$S_{1}与S_{2}$的数量关系是____;
(3)在四边形$ABCD$中,沿中点四边形$EFGH$的其中三边剪开,可得三个小三角形,将这三个小三角形与原图中未剪开的小三角形拼接成一个平行四边形,请画出一种拼接示意图,并写出对应全等的三角形。

答案:
(1)B;(2)$S_1=2S_2$;提示:如图1所示,△MBC中,易证K,P分别为MB,MC的中点,$S_{\triangle MFK}=S_{\triangle BFK}$,$S_{\triangle MFP}=S_{\triangle CFP}$,所以$S_{\triangle MBC}=2S_{□ MKFP}$;(3)答案合理即可,如图2所示,四边形NEHM是平行四边形;△MAH≌△GDH,△NAE≌△FBE,△CFG≌△ANM.
 (第23题图)
(第23题图)
(1)B;(2)$S_1=2S_2$;提示:如图1所示,△MBC中,易证K,P分别为MB,MC的中点,$S_{\triangle MFK}=S_{\triangle BFK}$,$S_{\triangle MFP}=S_{\triangle CFP}$,所以$S_{\triangle MBC}=2S_{□ MKFP}$;(3)答案合理即可,如图2所示,四边形NEHM是平行四边形;△MAH≌△GDH,△NAE≌△FBE,△CFG≌△ANM.

 (第23题图)
(第23题图) 查看更多完整答案,请扫码查看


