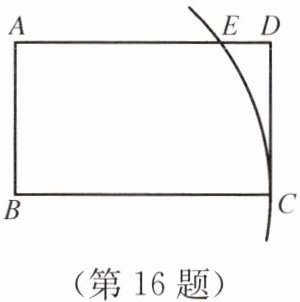
16. 如图所示,在矩形$ABCD$中,$\dfrac{AB}{BC}= \dfrac{3}{5}$,以点$B$为圆心,$BC$长为半径画弧,交边$AD于点E$。若$AE\cdot ED= \dfrac{4}{3}$,则矩形$ABCD$的面积为
5
。
答案:
5
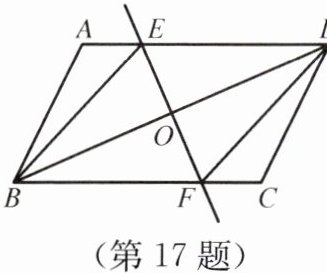
17. 如图所示,已知在$□ ABCD$中,$O为对角线BD$的中点,过点$O的直线EF分别交AD$、$BC于E$、$F$两点,连接$BE$、$DF$。
(1)求证:$\triangle DOE\cong\triangle BOF$;
(2)当$∠DOE$等于多少度时,四边形$BFDE$为菱形?请说明理由。
(1)求证:$\triangle DOE\cong\triangle BOF$;
(2)当$∠DOE$等于多少度时,四边形$BFDE$为菱形?请说明理由。

答案:
(1)证明:
∵ 在□ABCD中,O为对角线BD的中点,
∴ BO=DO,∠EDB=∠FBO.又
∵ ∠EOD=∠FOB,
∴ △DOE≌△BOF(ASA);(2)解:当∠DOE=90°时,四边形BFDE为菱形.理由:
∵ △DOE≌△BOF,
∴ BF=DE.又
∵ BF//DE,
∴ 四边形EBFD是平行四边形.
∵ ∠EOD=90°,
∴ EF⊥BD.
∴ 四边形BFDE为菱形.
∵ 在□ABCD中,O为对角线BD的中点,
∴ BO=DO,∠EDB=∠FBO.又
∵ ∠EOD=∠FOB,
∴ △DOE≌△BOF(ASA);(2)解:当∠DOE=90°时,四边形BFDE为菱形.理由:
∵ △DOE≌△BOF,
∴ BF=DE.又
∵ BF//DE,
∴ 四边形EBFD是平行四边形.
∵ ∠EOD=90°,
∴ EF⊥BD.
∴ 四边形BFDE为菱形.
18. 如图所示,已知$Rt\triangle ABC$中,$∠ABC= 90^{\circ}$,先把$\triangle ABC绕点B按顺时针方向旋转90^{\circ}至\triangle DBE$后,再把$\triangle ABC沿射线AB平移至\triangle FEG$,$DE$、$FG相交于点H$。
(1)判断线段$DE$、$FG$的位置关系,并说明理由;
(2)连接$CG$,求证:四边形$CBEG$是正方形。

(1)判断线段$DE$、$FG$的位置关系,并说明理由;
(2)连接$CG$,求证:四边形$CBEG$是正方形。

答案:
(1)DE⊥FG,理由:由旋转知DE⊥AC,由平移知GF//AC,所以DE⊥FG;(2)因为△FEG由△ABC平移所得,所以EG//BC,EG=BC.所以四边形CBEG是平行四边形.由∠FEG=∠ABC=90°,所以□CBEG是矩形.因为△DBE由△ABC旋转所得,所以BE=BC.所以矩形CBEG是正方形.
查看更多完整答案,请扫码查看


