《2025年暑假生活江苏人民出版社八年级数学》

23. 如图所示,将透明三角形纸片$PAB的直角顶点P$落在第四象限,顶点$A$、$B分别落在反比例函数y= \frac {k}{x}$图像的两支上,且$PB⊥x$轴,$PA⊥y$轴,垂足分别为$C$、$D$,线段$AB分别与x$轴、$y轴相交于点E$、$F$。已知$B(1,3)$。
(1)$k= $3；
(2)试说明：$AE= BF$；
解：∵点$B(1,3)$在反比例函数$y = \frac{k}{x}$图像上，$k = 3$，∴反比例函数解析式为$y=\frac{3}{x}$。设点$A$的坐标为$(a,\frac{3}{a})$。∵$PB⊥x$轴，$PA⊥y$轴，垂足分别为$C$、$D$，∴点$D$的坐标为$(0,\frac{3}{a})$，点$P$的坐标为$(1,\frac{3}{a})$，点$C$的坐标为$(1,0)$。∴$PB = 3-\frac{3}{a}$，$PC=-\frac{3}{a}$，$PA=1 - a$，$PD = 1$。∴$\frac{PC}{PB}=\frac{-\frac{3}{a}}{3-\frac{3}{a}}=\frac{1}{1 - a}$，$\frac{PD}{PA}=\frac{1}{1 - a}$。∴$\frac{PC}{PB}=\frac{PD}{PA}$。∵$\angle CPD=\angle BPA$，∴$\triangle PCD\sim\triangle PBA$。∴$\angle PCD=\angle PBA$。∴$CD// BA$。∵$BC// DE$，$AD// FC$，∴四边形$BCDE$、$ADCF$都是平行四边形。∴$BE = CD$，$AF=CD$。∴$BE = AF$。∴$AF + EF=BE + EF$，即$AE=BF$。
(3)当四边形$ABCD的面积为\frac {21}{4}$时,求点$P$的坐标。
解：∵四边形$ABCD$的面积$=S_{\triangle PAB}-S_{\triangle PCD}$，∴$\frac{1}{2}\cdot(3-\frac{3}{a})\cdot(1 - a)-\frac{1}{2}\cdot1\cdot(-\frac{3}{a})=\frac{21}{4}$。整理得$2a^{2}+3a = 0$，解得$a_{1}=0$（舍去），$a_{2}=-\frac{3}{2}$。∴点$P$的坐标为$(1,-2)$。

答案：
(1) 3
(2) 解：
∵点$B(1,3)$在反比例函数$y = \frac{k}{x}$图像上，$k = 3$，
∴反比例函数解析式为$y=\frac{3}{x}$。设点$A$的坐标为$(a,\frac{3}{a})$。
∵$PB⊥x$轴，$PA⊥y$轴，垂足分别为$C$、$D$，
∴点$D$的坐标为$(0,\frac{3}{a})$，点$P$的坐标为$(1,\frac{3}{a})$，点$C$的坐标为$(1,0)$。
∴$PB = 3-\frac{3}{a}$，$PC=-\frac{3}{a}$，$PA=1 - a$，$PD = 1$。
∴$\frac{PC}{PB}=\frac{-\frac{3}{a}}{3-\frac{3}{a}}=\frac{1}{1 - a}$，$\frac{PD}{PA}=\frac{1}{1 - a}$。
∴$\frac{PC}{PB}=\frac{PD}{PA}$。
∵$\angle CPD=\angle BPA$，
∴$\triangle PCD\sim\triangle PBA$。
∴$\angle PCD=\angle PBA$。
∴$CD// BA$。
∵$BC// DE$，$AD// FC$，
∴四边形$BCDE$、$ADCF$都是平行四边形。
∴$BE = CD$，$AF=CD$。
∴$BE = AF$。
∴$AF + EF=BE + EF$，即$AE=BF$。
(3) 解：
∵四边形$ABCD$的面积$=S_{\triangle PAB}-S_{\triangle PCD}$，
∴$\frac{1}{2}\cdot(3-\frac{3}{a})\cdot(1 - a)-\frac{1}{2}\cdot1\cdot(-\frac{3}{a})=\frac{21}{4}$。整理得$2a^{2}+3a = 0$，解得$a_{1}=0$（舍去），$a_{2}=-\frac{3}{2}$。
∴点$P$的坐标为$(1,-2)$。

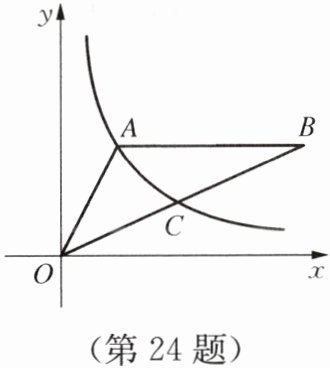
24. 如图所示,双曲线$y= \frac {k}{x}(x＞0)经过\triangle OAB的顶点A和OB的中点C$,$AB// x$轴,点$A的坐标为(2,3)$。
(1)确定$k$的值；
(2)若点$D(3,m)$在双曲线上,求直线$AD$的函数关系式；
(3)计算$\triangle OAB$的面积。

答案：  
(1)
∵双曲线$y = \frac{k}{x}(x＞0)$经过点$A(2,3)$，$\therefore 3=\frac{k}{2}$，解得$k = 6$。
(2)
∵点$D(3,m)$在双曲线$y=\frac{6}{x}$上，$\therefore m=\frac{6}{3}=2$，即$D(3,2)$。设直线$AD$的函数关系式为$y=ax + b$，将$A(2,3)$，$D(3,2)$代入得$\begin{cases}2a + b=3\\3a + b=2\end{cases}$，解得$\begin{cases}a=-1\\b = 5\end{cases}$，$\therefore$直线$AD$的函数关系式为$y=-x + 5$。
(3)
∵$AB// x$轴，$A(2,3)$，$\therefore$设$B(t,3)$，则$OB$的中点$C\left(\frac{t}{2},\frac{3}{2}\right)$。
∵点$C$在双曲线$y = \frac{6}{x}$上，$\therefore\frac{3}{2}=\frac{6}{\frac{t}{2}}$，解得$t = 8$，$\therefore B(8,3)$，$AB=8 - 2=6$。$\therefore S_{\triangle OAB}=\frac{1}{2}× AB×3=\frac{1}{2}×6×3 = 9$。