《2025年暑假生活江苏人民出版社八年级数学》

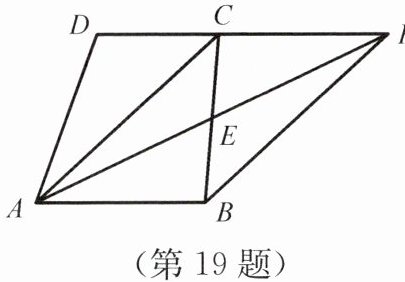
19. 如图所示,已知在四边形$ABCD$中,$AB// CD$,$E是BC$的中点,直线$AE交DC的延长线于点F$。试判断四边形$ABFC$的形状,并证明你的结论。

答案： 四边形$ABFC$是平行四边形。
证明：
$\because AB// CD$，
$\therefore \angle BAE = \angle CFE$。
$\because E$是$BC$的中点，
$\therefore CE = BE$。
在$\triangle CEF$和$\triangle BEA$中，
$\left\{\begin{array}{l}\angle CFE=\angle BAE\\\angle CEF=\angle BEA\\CE = BE\end{array}\right.$，
$\therefore \triangle CEF≌\triangle BEA(AAS)$，
$\therefore EA = EF$。
又$\because CE = BE$，
$\therefore$四边形$ABFC$是平行四边形。

20. 如图所示,已知在菱形$ABCD$中,$M$、$N分别是边AB$、$BC$的中点,$MP⊥AB交CD于点P$,连接$NM$、$NP$。
(1)若$∠B= 60^{\circ}$,这时点$P与点C$重合,则$∠NMP= $30$^{\circ}$；
(2)求证：$NM= NP$。

证明：延长$MN$交$DC$的延长线于点$E$。
∵四边形$ABCD$是菱形，
∴$AB// CD$，
∴$\angle BMN=\angle E$，$\angle MBN=\angle ECN$。
∵$N$是$BC$的中点，
∴$BN=CN$。
在$\triangle MNB$和$\triangle ENC$中，
$\left\{\begin{array}{l} \angle BMN=\angle E\\ \angle MBN=\angle ECN\\ BN=CN\end{array}\right.$
∴$\triangle MNB\cong\triangle ENC(AAS)$，
∴$MN=EN$。
∵$MP\perp AB$，$AB// CD$，
∴$MP\perp DE$，
∴$PN=\frac{1}{2}ME=MN$，
即$NM=NP$。

答案： （1）30
（2）证明：延长$MN$交$DC$的延长线于点$E$。
∵四边形$ABCD$是菱形，
∴$AB// CD$，
∴$\angle BMN=\angle E$，$\angle MBN=\angle ECN$。
∵$N$是$BC$的中点，
∴$BN=CN$。
在$\triangle MNB$和$\triangle ENC$中，
$\left\{\begin{array}{l} \angle BMN=\angle E\\ \angle MBN=\angle ECN\\ BN=CN\end{array}\right.$
∴$\triangle MNB\cong\triangle ENC(AAS)$，
∴$MN=EN$。
∵$MP\perp AB$，$AB// CD$，
∴$MP\perp DE$，
∴$PN=\frac{1}{2}ME=MN$，
即$NM=NP$。