《2025年暑假生活江苏人民出版社八年级数学》

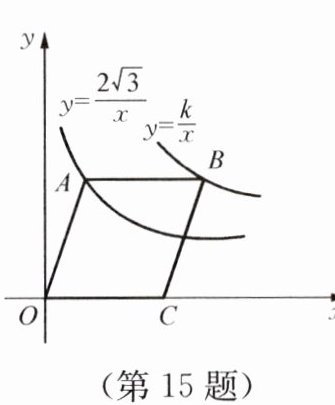
15. 如图所示,点$A在双曲线y= \frac {2\sqrt {3}}{x}(x＞0)$上,点$B在双曲线y= \frac {k}{x}(x＞0)$上(点$B在点A$的右侧),且$AB// x$轴,若四边形$OABC$是菱形,且$∠AOC= 60^{\circ }$,则$k= $$6\sqrt{3}$。

答案： 设点$ A $的坐标为$ (a, b) $，因为点$ A $在双曲线$ y = \frac{2\sqrt{3}}{x}(x ＞ 0) $上，所以$ ab = 2\sqrt{3} $。
由于$ AB // x $轴，点$ B $在点$ A $右侧，故点$ B $的纵坐标为$ b $，设点$ B $的坐标为$ (c, b) $，又因为点$ B $在双曲线$ y = \frac{k}{x}(x ＞ 0) $上，所以$ k = bc $。
因为四边形$ OABC $是菱形，所以$ OA = OC = AB $，且$ AB = c - a $。
过点$ A $作$ AD \perp x $轴于点$ D $，在$ Rt\triangle AOD $中，$ \angle AOC = 60^\circ $，则$ OA = \frac{AD}{\sin 60^\circ} = \frac{b}{\frac{\sqrt{3}}{2}} = \frac{2b}{\sqrt{3}} $，$ OD = a = OA \cos 60^\circ = \frac{2b}{\sqrt{3}} × \frac{1}{2} = \frac{b}{\sqrt{3}} $。
由$ ab = 2\sqrt{3} $，将$ a = \frac{b}{\sqrt{3}} $代入得：$ \frac{b}{\sqrt{3}} × b = 2\sqrt{3} $，即$ b^2 = 6 $，解得$ b = \sqrt{6} $（$ b ＞ 0 $）。
则$ OA = \frac{2\sqrt{6}}{\sqrt{3}} = 2\sqrt{2} $，所以$ AB = OA = 2\sqrt{2} $，即$ c - a = 2\sqrt{2} $。
又因为$ a = \frac{b}{\sqrt{3}} = \frac{\sqrt{6}}{\sqrt{3}} = \sqrt{2} $，所以$ c = a + 2\sqrt{2} = \sqrt{2} + 2\sqrt{2} = 3\sqrt{2} $。
因此$ k = bc = \sqrt{6} × 3\sqrt{2} = 3\sqrt{12} = 6\sqrt{3} $。
$ 6\sqrt{3} $

16. 如图所示,在平面直角坐标系中,点$A和点C分别在y轴和x$轴正半轴上,以$OA$、$OC为边作矩形OABC$,双曲线$y= \frac {6}{x}(x＞0)交AB于点E$,$AE:EB= 1:3$,则矩形$OABC$的面积是24。

答案： 24

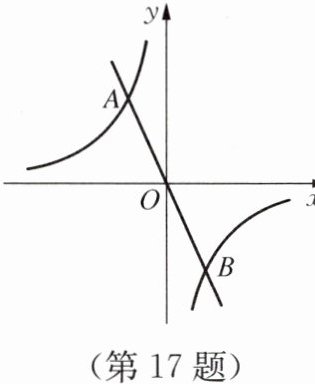
17. 如图所示,正比例函数$y= -2x与反比例函数y= \frac {k}{x}的图像相交于A(m,2)$、$B$两点。
(1)求反比例函数的表达式及点$B$的坐标；
(2)结合图像直接写出当$-2x＞\frac {k}{x}$时,$x$的取值范围。

答案：  
(1)把$A(m,2)$代入$y = -2x$得$-2m=2$，解得$m=-1$，所以点$A$的坐标为$(-1,2)$。把$A(-1,2)$代入$y=\frac{k}{x}$得$k=-1×2=-2$，所以反比例函数表达式为$y=-\frac{2}{x}$。因为点$A$与点$B$关于原点对称，所以点$B$的坐标为$(1,-2)$；
(2)$x ＜ -1$或$0 ＜ x ＜ 1$

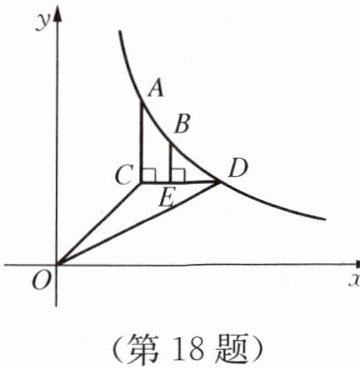
18. 如图所示,已知函数$y= \frac {k}{x}(x＞0)的图像经过点A$、$B$,点$A的坐标为(1,2)$,过点$A作AC// y$轴,$AC= 1$(点$C位于点A$的下方),过点$C作CD// x$轴,与函数的图像交于点$D$,过点$B作BE⊥CD$,垂足$E在线段CD$上,连接$OC$、$OD$。
(1)求$\triangle OCD$的面积；
(2)当$BE= \frac {1}{2}AC$时,求$CE$的长。

答案：
(1)
∵函数$y = \frac{k}{x}(x＞0)$的图像经过点$A(1,2)$，
$\therefore 2=\frac{k}{1}$，解得$k = 2$，
$\therefore$函数解析式为$y=\frac{2}{x}$，
$\because AC// y$轴，$AC = 1$，点$C$位于点$A$下方，$A(1,2)$，
$\therefore$点$C$的坐标为$(1,2 - 1)=(1,1)$，
$\because CD// x$轴，点$D$在函数$y=\frac{2}{x}$的图像上，
$\therefore$点$D$的纵坐标为$1$，
当$y = 1$时，$1=\frac{2}{x}$，解得$x = 2$，
$\therefore$点$D$的坐标为$(2,1)$，
$\therefore CD=2 - 1=1$，点$C$到$x$轴的距离为$1$，
$\therefore S_{\triangle OCD}=\frac{1}{2}× CD×1=\frac{1}{2}×1×1=\frac{1}{2}$；
(2)$\because AC = 1$，$BE=\frac{1}{2}AC$，
$\therefore BE=\frac{1}{2}×1=\frac{1}{2}$，
$\because CD// x$轴，点$C$的纵坐标为$1$，$BE\perp CD$，
$\therefore$点$B$的纵坐标为$1+\frac{1}{2}=\frac{3}{2}$，
$\because$点$B$在函数$y=\frac{2}{x}$的图像上，
$\therefore$当$y=\frac{3}{2}$时，$\frac{3}{2}=\frac{2}{x}$，解得$x=\frac{4}{3}$，
$\therefore$点$B$的坐标为$(\frac{4}{3},\frac{3}{2})$，
$\because E$在线段$CD$上，$CD$上点的横坐标范围是$1$到$2$，点$B$的横坐标为$\frac{4}{3}$，
$\therefore$点$E$的坐标为$(\frac{4}{3},1)$，
$\because$点$C$的坐标为$(1,1)$，
$\therefore CE=\frac{4}{3}-1=\frac{1}{3}$。