《2025年暑假生活江苏人民出版社八年级数学》

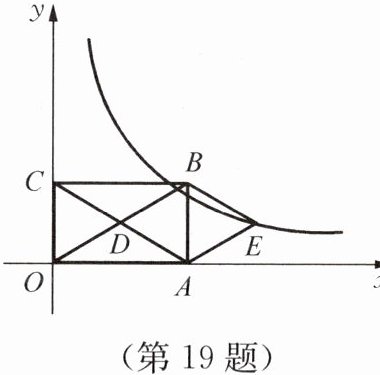
19. 如图所示,在平面直角坐标系中,矩形$OABC的对角线OB$、$AC相交于点D$,且$BE// AC$,$AE// OB$。
(1)求证：四边形$AEBD$是菱形；
(2)若$OA= 3$,$OC= 2$,求出经过点$E$的反比例函数表述式。

答案： 1. （1）证明：
因为$BE// AC$，$AE// OB$，所以四边形$AEBD$是平行四边形。
又因为四边形$OABC$是矩形，所以$OB = AC$，$OD=\frac{1}{2}OB$，$AD=\frac{1}{2}AC$，则$OD = AD$。
所以$\angle OBD=\angle ADB$，因为$AE// OB$，所以$\angle EAD=\angle ADB$，$\angle AED=\angle OBD$，则$\angle EAD=\angle AED$。
所以$AD = AE$，又因为四边形$AEBD$是平行四边形，所以四边形$AEBD$是菱形。
2. （2）解：
连接$DE$，交$AB$于$F$。
因为四边形$AEBD$是菱形，所以$AB$与$DE$互相垂直平分。
已知$OA = 3$，$OC = 2$，则$A(3,0)$，$B(3,2)$，所以$F(3,1)$。
因为$D$是$OB$中点，$O(0,0)$，$B(3,2)$，所以$D(\frac{3}{2},1)$。
因为$F$是$DE$中点，设$E(x,y)$，根据中点坐标公式$\frac{x+\frac{3}{2}}{2}=3$，$\frac{y + 1}{2}=1$。
由$\frac{x+\frac{3}{2}}{2}=3$，得$x+\frac{3}{2}=6$，$x=\frac{9}{2}$；由$\frac{y + 1}{2}=1$，得$y+1 = 2$，$y = 1$，所以$E(\frac{9}{2},1)$。
设反比例函数表达式为$y=\frac{k}{x}(k\neq0)$，把$E(\frac{9}{2},1)$代入$y=\frac{k}{x}$，得$k=\frac{9}{2}×1=\frac{9}{2}$。
所以反比例函数表达式为$y = \frac{9}{2x}$。
综上，（1）得证；（2）反比例函数表达式为$y=\frac{9}{2x}$。

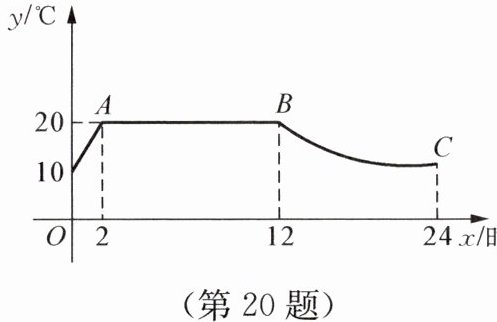
20. 某市某蔬菜生产基地用装有恒温系统的大棚栽培一种适宜生长温度为$15\sim 20^{\circ }C$的新品种,如图所示是某天恒温系统从开启到关闭及关闭后,大棚里温度$y(^{\circ }C)随时间x$(时)变化的函数图像,其中$AB$段是恒温阶段,$BC段是双曲线y= \frac {k}{x}$的一部分,请根据图中信息解答下列问题：
(1)求$k$的值；
(2)恒温系统在一天内保持大棚里温度在$15^{\circ }C及15^{\circ }C$以上的时间有多少小时？

答案： 1. （1）
因为$BC$段是双曲线$y = \frac{k}{x}$的一部分，且点$B(12,20)$在双曲线$y=\frac{k}{x}$上。
根据反比例函数$y = \frac{k}{x}$（$k\neq0$）的性质，当$x = 12$，$y = 20$时，把$x = 12$，$y = 20$代入$y=\frac{k}{x}$中，可得$k=xy$。
所以$k = 12×20=240$。
2. （2）
设$AD$段的函数解析式为$y = mx + n$（$m\neq0$），已知$A(2,20)$，$D(0,10)$。
把$\begin{cases}x = 0,y = 10\\x = 2,y = 20\end{cases}$代入$y=mx + n$中，得$\begin{cases}n = 10\\2m + n = 20\end{cases}$。
将$n = 10$代入$2m + n = 20$，得$2m+10 = 20$，$2m=10$，解得$m = 5$。
所以$AD$段的函数解析式为$y = 5x + 10$。
当$y = 15$时，在$AD$段：$15 = 5x + 10$，$5x=5$，解得$x = 1$；
在$BC$段：因为$y=\frac{240}{x}$，当$y = 15$时，$15=\frac{240}{x}$，解得$x=\frac{240}{15}=16$。
所以恒温系统在一天内保持大棚里温度在$15^{\circ}C$及$15^{\circ}C$以上的时间为$16 - 1=15$小时。
综上，（1）$k = 240$；（2）$15$小时。