《2025年一遍过七年级数学上册苏科版》

若 $ n $ 表示一个奇数,则下面各数中表示偶数的是(A)
A.$ 2n $
B.$ n + 2 $
C.$ 2n + 1 $
D.$ 2n - 1 $

答案： A

买一个足球需要 $ m $ 元,买一个篮球需要 $ n $ 元,则买 6 个足球和 3 个篮球共需B
A.$ 18m $ 元
B.$ (6m + 3n) $ 元
C.$ (3m + 6n) $ 元
D.$ 9m $ 元

答案： B

3 [2025 镇江期中]$ m $ 是一个三位数,$ n $ 是一个两位数,若把 $ n $ 放在 $ m $ 的左边,组成一个五位数,则这个五位数是1000n + m.

答案： 1000n + m

如下是一张月历表,省去了具体日期,设①位置上的数表示为 $ a $,则②位置上的数可表示为a + 9.

答案： a + 9 由题图,得②位置上的数可表示为a + 7 + 2 = a + 9.

5 天星原创 用字母表示下列运算或数量关系:
(1)一个数的 2 倍减 2 后大于这个数;
(2)两个数的和乘 3 的积的倒数.

答案： 解:
(1)设这个数为x. “一个数的2倍减2后大于这个数” 字母表示数可表示为2x - 2 ＞ x.
(2)设这两个数为a,b. “两个数的和乘3的积的倒数”可表示为$\frac{1}{3(a+b)}$.

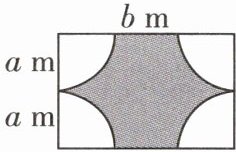
6 如图所示的是某居民小区的一块长为 $ b $ m,宽为 $ 2a $ m 的长方形空地. 为了美化环境,在这个长方形空地的四个顶点各修建了一个半径为 $ a $ m 的扇形花坛,然后在花坛内种花,其余空地种草. 如果种花每平方米需要资金 200 元,种草每平方米需要资金 150 元,那么美化这块空地共需资金多少元? (不需要化简)
]

答案： 解:长方形空地的面积为2ab$m^2$,四个扇形花坛的面积为$4×\frac{1}{4}\pi a^2=\pi a^2$($m^2$), 所以中间阴影部分(种草区域)的面积为$(2ab - \pi a^2)m^2$,因此美化这块空地共需资金$[200×\pi a^2 + (2ab - \pi a^) × (2ab - \pi a^)]$元.

观察下列式子:$ 1 ^ { 2 } - 1 = 1 × 0 $;$ 2 ^ { 2 } - 2 = 2 × 1 $;$ 3 ^ { 2 } - 3 = 3 × 2 $;$ 4 ^ { 2 } - 4 = 4 × 3 $;$ 5 ^ { 2 } - 5 = 5 × 4 $;…$$. 用字母 $ n $ ($ n $ 为正整数)表示一般规律为______$n^2 - n = n(n - 1)$.

答案： $n^2 - n = n(n - )$

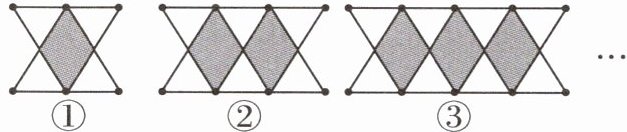
8 [2023 十堰中考]用火柴棍拼成如图图案,其中第①个图案由 4 个小等边三角形围成 1 个小平行四边形,第②个图案由 6 个小等边三角形围成 2 个小平行四边形形……$$若按此规律拼下去,则第 $ n $ 个图案需要火柴棍的根数为______.(用含 $ n $ 的式子表示)
]

6n + 6

答案： 6n + 6

9 有一棵树苗,刚栽下去时,树高为 1.8 m,一年后树高为 2.2 m,两年后树高为 2.6 m,三年后树高为 3.0 m……$$按照这样的规律,$ n $ 年后(理想状态下)树高为多少?

答案： 解:刚栽下去时,树高为m; 一年后树高为m; 两年后树高为m; …… 则n年后树高为m.