第25页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
10已知两个有理数a,b,如果$ab<0$,且$a+b<0$,那么(
A.$a>0,b>0$
B.$a<0,b>0$
C.a,b异号
D.a,b异号,且负数的绝对值较大
D
)A.$a>0,b>0$
B.$a<0,b>0$
C.a,b异号
D.a,b异号,且负数的绝对值较大
答案:
D 两个有理数相乘的积是负数,说明两数异号,和也是负数,说明负数的绝对值大于正数的绝对值.
11如图,A,B两点在数轴上表示的数分别为a,b,下列式子成立的是(
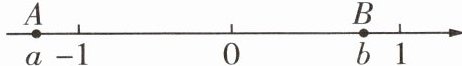
A.$ab>0$
B.$a+b>0$
C.$(b-1)(a+1)<0$
D.$(b-1)(a-1)>0$
D
)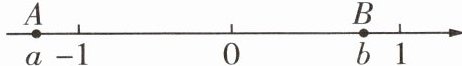
A.$ab>0$
B.$a+b>0$
C.$(b-1)(a+1)<0$
D.$(b-1)(a-1)>0$
答案:
D 由题图,知-2<a<-1,0<b<1,所以ab<0,故A不符合题意;a+b<0,故B不符合题意;因为b-1<0,a+1<0,所以(b-1)(a+1)>0,故C不符合题意;因为a-1<0,b-1<0,所以(b-1)(a-1)>0,故D符合题意.
12如图,按以下规律,第四个正方形内应填入的数是
210
.
答案:
210 由题中前面三个正方形的规律可知,第四个正方形内的数应是它的四个角上的数的乘积,即(-1)×(-5)×(-6)×(-7)=210.
13计算:
(1)$(-3)×\frac {5}{6}×(-1\frac {4}{5})×(-\frac {1}{4})$;
(2)$(-10)×|-3|×(-\frac {1}{2})×(-5\frac {1}{3})$.
(1)$(-3)×\frac {5}{6}×(-1\frac {4}{5})×(-\frac {1}{4})$;
(2)$(-10)×|-3|×(-\frac {1}{2})×(-5\frac {1}{3})$.
答案:
解:
(1)$(-3)× \frac{5}{6}× (-1\frac{4}{5})× (-\frac{1}{4})$
$=(-\frac{5}{2})× (-\frac{9}{5})× (-\frac{1}{4})$
$=\frac{9}{2}× (-\frac{1}{4})$
$=-\frac{9}{8}$.
(2)$(-10)× \vert -3\vert × (-\frac{1}{2})× (-5\frac{1}{3})$
$=(-10)× 3× (-\frac{1}{2})× (-5\frac{1}{3})$
$=-(10× 3× \frac{1}{2}× \frac{16}{3})$
=-80.
(1)$(-3)× \frac{5}{6}× (-1\frac{4}{5})× (-\frac{1}{4})$
$=(-\frac{5}{2})× (-\frac{9}{5})× (-\frac{1}{4})$
$=\frac{9}{2}× (-\frac{1}{4})$
$=-\frac{9}{8}$.
(2)$(-10)× \vert -3\vert × (-\frac{1}{2})× (-5\frac{1}{3})$
$=(-10)× 3× (-\frac{1}{2})× (-5\frac{1}{3})$
$=-(10× 3× \frac{1}{2}× \frac{16}{3})$
=-80.
14小明同学在自学了简单的电脑编程后,设计了如图所示的程序.
(1)若输入的数是-4,则执行程序后,输出的数是多少?
(2)若输入的数是2,则执行程序后,输出的数是多少?
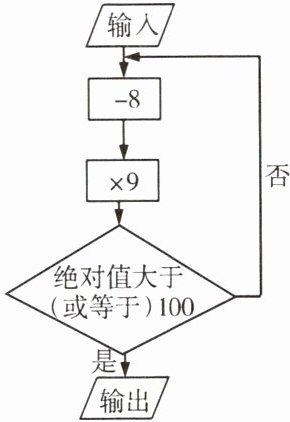
(1)若输入的数是-4,则执行程序后,输出的数是多少?
(2)若输入的数是2,则执行程序后,输出的数是多少?

答案:
解:
(1)因为(-4-8)×9=-12×9=-108,|-108|=108>100,故输出的数是-108.
(2)因为(2-8)×9=-54,|-54|=54<100,所以再把-54输入,得(-54-8)×9=-558,|-558|=558>100,故输出的数是-558.
(1)因为(-4-8)×9=-12×9=-108,|-108|=108>100,故输出的数是-108.
(2)因为(2-8)×9=-54,|-54|=54<100,所以再把-54输入,得(-54-8)×9=-558,|-558|=558>100,故输出的数是-558.
15新趋势·代数推理点A,B,C在数轴上的位置如图所示.有理数m,n,p对应着A,B,C三点中的某一点,且$mn<0,m+n>0,mp>np$,则数轴上点A,B,C中哪个点表示有理数n?
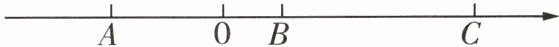
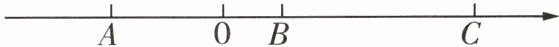
答案:
解:因为mn<0,m+n>0,所以m和n异号,由数轴可知m,n,p中有两个正数,一个负数,所以p为正数.因为mp>np,所以m>n,所以n为负数,所以数轴上点A表示有理数n.
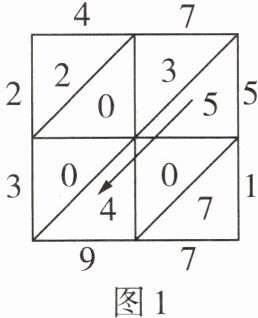
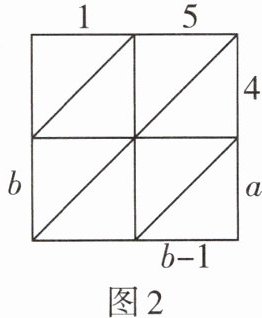
16新情境推理能力[2025苏州工业园区期末]“格子乘法”作为两个数相乘的一种计算方法最早在15世纪由意大利数学家帕乔利提出,在明代的《算法统宗》一书中被称为“铺地锦”,如图1,计算$47×51$,将乘数47计入上行,乘数51计入右行,然后以乘数47的每位数乘乘数51的每位数,将结果计入相应的格子中,最后按斜行加起来(斜行的和均小于10),得2397.如图2,用“铺地锦”的方法表示两个两位数相乘,这两个两位数相乘的结果为____.


答案:
615或645或675 由题图,得1×4=4,5×4=20,1·a=a,如图1,所以b=6,所以如图2,a应为奇数1,3,5,7,9.所以两个两位数可以为15×41;15×43;15×45;15×47;15×49,当a=1,3,5时,满足斜行的和均小于10;当a=7,9时,不满足斜行的和均小于10,所以相乘的结果为615或645或675.


615或645或675 由题图,得1×4=4,5×4=20,1·a=a,如图1,所以b=6,所以如图2,a应为奇数1,3,5,7,9.所以两个两位数可以为15×41;15×43;15×45;15×47;15×49,当a=1,3,5时,满足斜行的和均小于10;当a=7,9时,不满足斜行的和均小于10,所以相乘的结果为615或645或675.


查看更多完整答案,请扫码查看


