《2025年暑假作业知识出版社七年级数学华师大版》

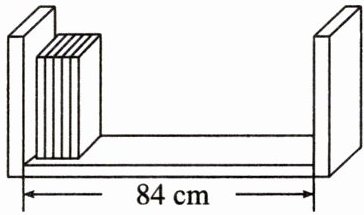
9. 如图,书架宽 $ 84 \mathrm { cm } $,在该书架上按图示方式摆放数学书和语文书,已知每本数学书厚 $ 0.8 \mathrm { cm } $,每本语文书厚 $ 1.2 \mathrm { cm } $.如果书架上已摆放 $ 10 $ 本语文书,那么数学书最多还可以摆多少本?

解 设数学书还可以摆 $x$ 本.
根据题意,得 $1.2 × 10 + 0.8x \leq 84$,
解得 $x \leq 90$.
答:数学书最多还可以摆90本.

答案： 解 设数学书还可以摆 $x$ 本.
根据题意,得 $1.2 × 10 + 0.8x \leq 84$,
解得 $x \leq 90$.
答:数学书最多还可以摆 90 本.

10. 关于 $ x $ 的不等式 $ 4 x - a ＞ 7 x + 5 $ 的解集是 $ x ＜ - 1 $,则 $ a $ 等于(A)
A. $ - 2 $ B. $ 2 $ C. $ 8 $ D. $ 5 $

答案： A

11. 关于 $ x $ 的不等式 $ m - \frac { x } { 2 } \leq 1 - x $ 有正数解,$ m $ 的值可以是______0(答案不唯一)(写出一个即可).

答案： 0(答案不唯一)

12. 关于 $ x $ 的不等式 $ 3 x - a \leq 0 $ 只有 $ 3 $ 个正整数解,则 $ a $ 的取值范围是$9 \leq a ＜ 12$.

答案： $9 \leq a ＜ 12$

13. 某中学组织本校师生参加红色研学实践活动,现租用甲、乙两种客车(每种客车至少 $ 1 $ 辆)送 $ 549 $ 名学生和 $ 11 $ 名教师到实践活动开展地,每辆客车上至少要有 $ 1 $ 名教师.甲、乙两种客车的载客量和租金如下表所示.
(1)共需租用多少辆客车? 11辆
(2)最多可以租用多少辆甲种客车? 3辆
(3)有几种租车方案? 哪种租车方案最省钱? 有3种租车方案，租用3辆甲种客车，8辆乙种客车最省钱

答案： 解
(1)因为 $549 + 11 = 560$(名),$560 ÷ 55 = 10$(辆)$\cdots\cdots10$(名),
所以最少需租用 11 辆客车.
又因为每辆客车上至少要有 1 名教师,
所以共需租用 11 辆客车.
(2)设租用甲种客车 $x$ 辆,则租用乙种客车 $(11 - x)$ 辆.
根据题意,得 $40x + 55(11 - x) \geq 560$,解得 $x \leq 3$. 所以最多可以租用 3 辆甲种客车.
(3)由
(2)知 $x \leq 3$,且 $x$ 为正整数,
所以 $x$ 可取 1,2,3.
故有 3 种租车方案.
方案 1:租用 1 辆甲种客车,10 辆乙种客车.
方案 2:租用 2 辆甲种客车,9 辆乙种客车.
方案 3:租用 3 辆甲种客车,8 辆乙种客车.
方案 1 所需租车费用为 $500 × 1 + 600 × 10 = 6500$(元);
方案 2 所需租车费用为 $500 × 2 + 600 × 9 = 6400$(元);
方案 3 所需租车费用为 $500 × 3 + 600 × 8 = 6300$(元).
$6300 ＜ 6400 ＜ 6500$,故方案 3 最省钱.