《2025年暑假作业知识出版社七年级数学华师大版》

1. 下列不等式中,属于一元一次不等式的是(A)
A. $ 2 ( 1 - x ) + x ＞ 4 x - 2 $ B. $ x ^ { 2 } - 2 x + 1 ＞ 0 $
C. $ \frac { 1 } { 2 } + \frac { 1 } { 3 } ＞ \frac { 1 } { 6 } $ D. $ x + y ＞ 2 x + 2 $

答案： A

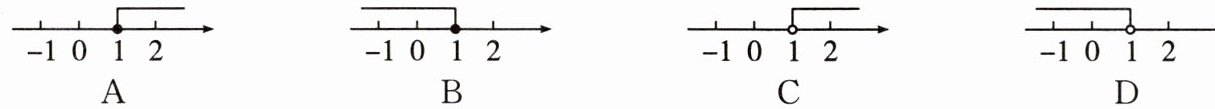
2. 不等式 $ x + 1 \geq 2 $ 的解集在数轴上表示为(A)

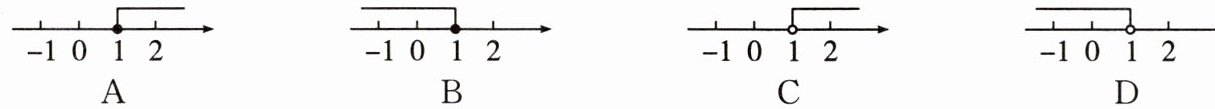
答案： A

3. 若 $ 2 a - x ^ { | 2 + 3 a | } ＞ 2 $ 是关于 $ x $ 的一元一次不等式,则 $ a $ 的值是(C)
A. $ - 1 $ B. $ 1 $ 或 $ - \frac { 1 } { 3 } $ C. $ - 1 $ 或 $ - \frac { 1 } { 3 } $ D. $ - \frac { 1 } { 3 } $

答案： C

4. 不等式 $ \frac { x - 7 } { 2 } + 1 ＜ \frac { 3 x - 2 } { 2 } $ 的负整数解有(B)
A. $ 0 $ 个 B. $ 1 $ 个 C. $ 2 $ 个 D. $ 4 $ 个

答案： B

5. 足球比赛规定:胜一场得 $ 3 $ 分,平一场得 $ 1 $ 分,负一场得 $ 0 $ 分.已知某队一共比赛了 $ 10 $ 场,均保持不败,得分超过 $ 22 $ 分,则该队(D)
A. 最多胜了 $ 6 $ 场 B. 最多胜了 $ 7 $ 场 C. 最少胜了 $ 6 $ 场 D. 最少胜了 $ 7 $ 场

答案： D

6. 当 $ x $ ＞\frac{3}{5}时,$ 5 x - 3 $ 的值是正数.

答案： $＞\frac{3}{5}$

7. 某商品进价 $ 4 $ 元,标价 $ 5 $ 元出售,商家准备打折销售,但其利润率不能少于 $ 10 \% $,则最多可打八八折.

答案： 八八

8. 解不等式,并把解集在数轴上表示出来.
(1)$ 2 ( x - 3 ) - 2 \leq 0 $;(2)$ \frac { x - 1 } { 2 } ＜ x + 1 $;(3)$ \frac { x + 1 } { 3 } - 1 \leq \frac { 2 - x } { 2 } $.

答案：
解
(1)去括号,得 $2x - 6 - 2 \leq 0$.
移项、合并同类项,得 $2x \leq 8$.
系数化为 1,得 $x \leq 4$.
这个不等式的解集在数轴上的表示如图所示.

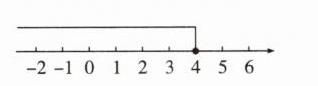
(2)去分母,得 $x - 1 ＜ 2(x + 1)$,
去括号,得 $x - 1 ＜ 2x + 2$,
移项,得 $-1 - 2 ＜ 2x - x$,
合并同类项,得 $x ＞ -3$.
这个不等式的解集在数轴上的表示如图所示.

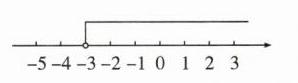
(3)去分母,得 $2(x + 1) - 6 \leq 3(2 - x)$,
去括号,得 $2x + 2 - 6 \leq 6 - 3x$,
移项,得 $2x + 3x \leq 6 + 6 - 2$,
合并同类项,得 $5x \leq 10$,
系数化为 1,得 $x \leq 2$.
这个不等式的解集在数轴上的表示如图所示.