2025年文涛书业假期作业快乐暑假八年级数学北师大版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年文涛书业假期作业快乐暑假八年级数学北师大版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
1. 下列多项式能因式分解的是(
A. $ m^{2}+n $
B. $ m^{2}-m+1 $
C. $ m^{2}-2 m+1 $
D. $ m^{2}-n $
C
)A. $ m^{2}+n $
B. $ m^{2}-m+1 $
C. $ m^{2}-2 m+1 $
D. $ m^{2}-n $
答案:
C
2. 如图,在$ □ A B C D $中,下列结论一定正确的是(
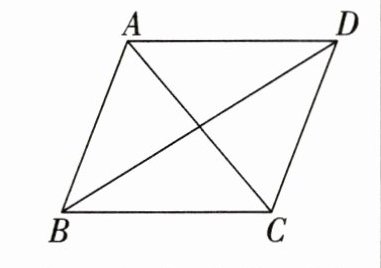
A. $ A C=B D $
B. $ A C \perp B D $
C. $ A B=C D $
D. $ A B=B C $
C
) 
A. $ A C=B D $
B. $ A C \perp B D $
C. $ A B=C D $
D. $ A B=B C $
答案:
C
3. 若等腰三角形有两条边的长度分别为3、1,则此等腰三角形的周长为(
A. 5
B. 7
C. 5或7
D. 6
B
)A. 5
B. 7
C. 5或7
D. 6
答案:
B
4. 在$ □ A B C D $中,$ \angle A: \angle B: \angle C: \angle D $的值可能是(
A. $ 2: 5: 2: 5 $
B. $ 3: 4: 4: 5 $
C. $ 4: 4: 3: 2 $
D. $ 2: 3: 5: 6 $
A
)A. $ 2: 5: 2: 5 $
B. $ 3: 4: 4: 5 $
C. $ 4: 4: 3: 2 $
D. $ 2: 3: 5: 6 $
答案:
A
5. 如图,在$ \triangle A B C $中,$ B D $平分$ \angle A B C $,$ C D $平分$ \angle A C E $,则$ \angle A $与$ \angle D $的关系是(
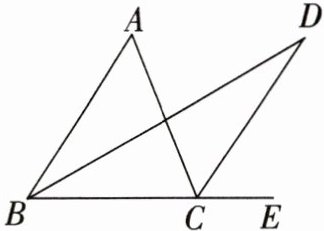
A. $ \angle D=\frac{1}{2} \angle A $
B. $ \angle D=90^{\circ}-\angle A $
C. $ \angle A+2 \angle D=90^{\circ} $
D. 不能确定
A
)
A. $ \angle D=\frac{1}{2} \angle A $
B. $ \angle D=90^{\circ}-\angle A $
C. $ \angle A+2 \angle D=90^{\circ} $
D. 不能确定
答案:
A
6. 在四边形$ A B C D $中,$ A D // B C $,要判定四边形$ A B C D $是平行四边形,那么还应满足(
A. $ \angle A+\angle C=180^{\circ} $
B. $ \angle B+\angle D=180^{\circ} $
C. $ \angle A+\angle B=180^{\circ} $
D. $ \angle A+\angle D=180^{\circ} $
D
)A. $ \angle A+\angle C=180^{\circ} $
B. $ \angle B+\angle D=180^{\circ} $
C. $ \angle A+\angle B=180^{\circ} $
D. $ \angle A+\angle D=180^{\circ} $
答案:
D
7. 如图,在$ \triangle A B C $中,$ \angle C=90^{\circ} $,$ A B $的垂直平分线$ D E $交$ A B $于点$ E $,交$ B C $于点$ D $. 若$ A B=13 $,$ A C=5 $,则$ \triangle A C D $的周长为(
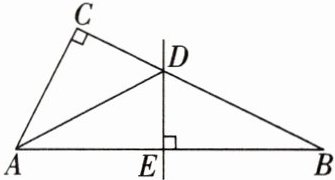
A. 18
B. 17
C. 20
D. 25
B
)
A. 18
B. 17
C. 20
D. 25
答案:
B
8. 点$ A 、 B 、 C $是平面内不在同一条直线上的三点,点$ D $是平面内任意一点. 若$ A 、 B 、 C 、 D $四点恰能构成一个平行四边形,则在平面内符合这样条件的点$ D $有(
A. 1个
B. 2个
C. 3个
D. 4个
C
)A. 1个
B. 2个
C. 3个
D. 4个
答案:
C
9. 关于$ x $的不等式$ 2(x-1)>4 $的解集为
$ x > 3 $
.
答案:
$ x > 3 $
10. 如图,在$ □ A B C D $中,$ A D=8 $,点$ E 、 F $分别是$ B D 、 C D $的中点,则$ E F= $
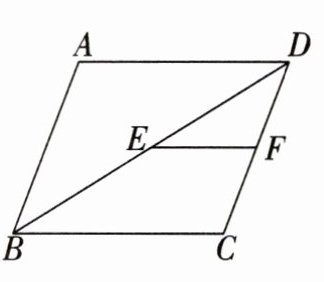
4
.
答案:
4
11. 已知$ O $是锐角$ \triangle A B C $三边垂直平分线的交点,且$ \angle A=50^{\circ} $,则$ \angle B O C $的度数是
$ 100^{\circ} $
.
答案:
$ 100^{\circ} $
12. 甲、乙两名同学分解因式$ x^{2}+a x+b $时,甲看错了$ b $,分解结果为$ (x+2) \cdot (x+4) $;乙看错了$ a $,分解结果为$ (x+1)(x+9) $,则$ a+b= $__________
15
.
答案:
15
13. 如图,$ A D $是$ \angle B A C $的平分线,$ D E \perp A B $,垂足为$ E $,$ D F \perp A C $,垂足为$ F $,且$ D B=D C $,求证:$ B E=C F $.
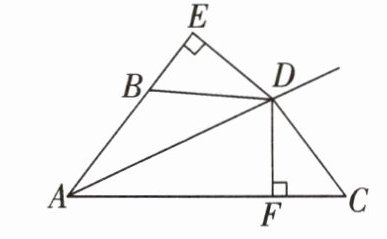
证明:∵ AD 是 $ \angle BAC $ 的平分线,$ DE \perp AB $,$ DF \perp AC $,∴ $ DE = DF $.
∵ $ DB = DC $,
∴ $ \triangle BDE \cong \triangle CDF $(

证明:∵ AD 是 $ \angle BAC $ 的平分线,$ DE \perp AB $,$ DF \perp AC $,∴ $ DE = DF $.
∵ $ DB = DC $,
∴ $ \triangle BDE \cong \triangle CDF $(
HL
),∴ $ BE = CF $.
答案:
证明:
∵ AD 是 $ \angle BAC $ 的平分线,$ DE \perp AB $,$ DF \perp AC $,
∴ $ DE = DF $.
∵ $ DB = DC $,
∴ $ \triangle BDE \cong \triangle CDF (HL) $,
∴ $ BE = CF $.
∵ AD 是 $ \angle BAC $ 的平分线,$ DE \perp AB $,$ DF \perp AC $,
∴ $ DE = DF $.
∵ $ DB = DC $,
∴ $ \triangle BDE \cong \triangle CDF (HL) $,
∴ $ BE = CF $.
查看更多完整答案,请扫码查看


