搜索
2025年文涛书业假期作业快乐暑假八年级数学北师大版
注：目前有些书本章节名称可能整理的还不是很完善，但都是按照顺序排列的，请同学们按照顺序仔细查找。练习册 2025年文涛书业假期作业快乐暑假八年级数学北师大版 答案主要是用来给同学们做完题方便对答案用的，请勿直接抄袭。
11. 解不等式组
并在数轴上表示不等式组的解集.
并在数轴上表示不等式组的解集.$ -1 \leq x ＜ \frac{5}{2} $
图略
答案：
$ -1 \leq x ＜ \frac{5}{2} $ 图略
12. 如图，在平行四边形ABCD中，$∠BCD$的平分线与 BA 的延长线相交于点 E，$BH⊥EC$于点 H，求证：$CH=EH$.
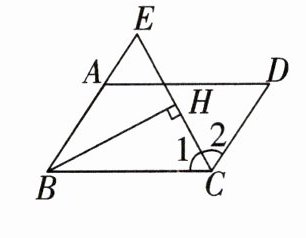
证明：∵ 在 $ □ ABCD $ 中，
∴ $ \angle E = \angle 2 $. ∵ $ CE $ 平分 $ \angle BCD $，
∴ $ \angle 1 = \angle 2 $，∴ $ \angle 1 = \angle E $，
∴
又 ∵ $ BH \perp EC $，∴ $ CH = EH $（
证明：∵ 在 $ □ ABCD $ 中，
$BE // CD$
，∴ $ \angle E = \angle 2 $. ∵ $ CE $ 平分 $ \angle BCD $，
∴ $ \angle 1 = \angle 2 $，∴ $ \angle 1 = \angle E $，
∴
$BE = BC$
.又 ∵ $ BH \perp EC $，∴ $ CH = EH $（
三线合一
）.
答案：
证明：
∵ 在 $ \square ABCD $ 中，$ BE // CD $，
∴ $ \angle E = \angle 2 $.
∵ $ CE $ 平分 $ \angle BCD $，
∴ $ \angle 1 = \angle 2 $，
∴ $ \angle 1 = \angle E $，
∴ $ BE = BC $.
又
∵ $ BH \perp EC $，
∴ $ CH = EH $（三线合一）.
∵ 在 $ \square ABCD $ 中，$ BE // CD $，
∴ $ \angle E = \angle 2 $.
∵ $ CE $ 平分 $ \angle BCD $，
∴ $ \angle 1 = \angle 2 $，
∴ $ \angle 1 = \angle E $，
∴ $ BE = BC $.
又
∵ $ BH \perp EC $，
∴ $ CH = EH $（三线合一）.
13. 如图，$△A_{1}B_{1}C_{1}$是$△ABC$向右平移 4 个单位长度后得到的，且三个顶点的坐标分别为$A_{1}(1,1),B_{1}(4,2),C_{1}(3,4);$
(1) 请画出$△ABC$，并写出点 A、B、C 的坐标；A(
(2) 求出$△AOA_{1}$的面积.
(1) 请画出$△ABC$，并写出点 A、B、C 的坐标；A(
-3,1
)，B(0,2
)，C(-1,4
)(2) 求出$△AOA_{1}$的面积.
2
答案：
解：
(1) 图略，$ A(-3,1) $，$ B(0,2) $，$ C(-1,4) $.
(2) $ S_{\triangle AOA_1} = \frac{1}{2} \times 4 \times 1 = 2 $.
(1) 图略，$ A(-3,1) $，$ B(0,2) $，$ C(-1,4) $.
(2) $ S_{\triangle AOA_1} = \frac{1}{2} \times 4 \times 1 = 2 $.
查看更多完整答案，请扫码查看
