《2025年文涛书业假期作业快乐暑假八年级数学北师大版》

11. 不等式组$\begin{cases}x ＞ a,\\x ＜ 3\end{cases}$的整数解有三个，则$a$的取值范围是$-1 \leq a ＜ 0$.

答案： $-1 \leq a ＜ 0$

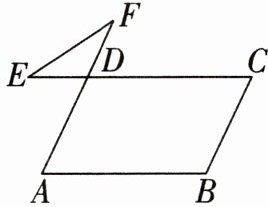
12. 如图，在$□ ABCD$中，$\angle B = 115^{\circ}$，延长$AD$至点$F$，延长$CD$至点$E$，连接$EF$，则$\angle E + \angle F =$$65^{\circ}$.

答案： $65^{\circ}$

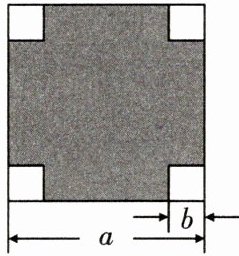
13. 如图，在一块边长为$a\ cm$的正方形纸板四角，各剪去一个边长为$b\ cm$（$b ＜ \frac{a}{2}$）的正方形，利用因式分解计算，当$a = 13.2$，$b = 3.4$时剩余部分的面积为128$cm^{2}$.

答案： 解：$a^{2} - 4b^{2} = (a + 2b)(a - 2b) = 20 \times 6.4 = 128(cm^{2})$

14. 如图，点$D$在$AC$上，点$E$在$AB$上，且$AB = AC$，$BC = BD$，$AD = DE = BE$，求$\angle A$的度数.

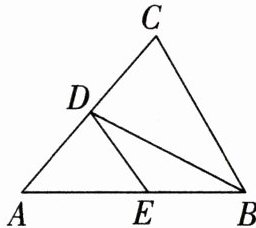
解：设$∠A = x$，$\because AD = DE = BE$，$\therefore ∠DEA = ∠A = x$，$∠EBD = ∠EDB$，又$\because ∠DEA = ∠EBD + ∠EDB$，$\therefore ∠EBD = ∠EDB = \frac{1}{2}x$，$\therefore ∠BDC = ∠A + ∠ABD = \frac{3}{2}x$。$\because BD = BC$，$AB = AC$，$\therefore ∠BDC = ∠BCD = ∠ABC = \frac{3}{2}x$，在$\triangle ABC$中，$∠A + ∠ABC + ∠ACB = 180^{\circ}$，$\therefore x + \frac{3}{2}x + \frac{3}{2}x = 180^{\circ}$，$\therefore x = 45^{\circ}$，即$∠A = $$45^{\circ}$。

答案： 解：设$∠A = x$，$\because AD = DE = BE$，
$\therefore ∠DEA = ∠A = x$，$∠EBD = ∠EDB$，
又$\because ∠DEA = ∠EBD + ∠EDB$，
$\therefore ∠EBD = ∠EDB = \frac{1}{2}x$，
$\therefore ∠BDC = ∠A + ∠ABD = \frac{3}{2}x$。
$\because BD = BC$，$AB = AC$，
$\therefore ∠BDC = ∠BCD = ∠ABC = \frac{3}{2}x$，
在$\triangle ABC$中，$∠A + ∠ABC + ∠ACB = 180^{\circ}$，
$\therefore x + \frac{3}{2}x + \frac{3}{2}x = 180^{\circ}$，
$\therefore x = 45^{\circ}$，即$∠A = 45^{\circ}$。