第58页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
7. 某中学七年级数学社团随机抽取部分学生,对“学习习惯”进行问卷调查。
设计问题:对自己做错的题目进行整理、分析、改正。
答案选项:很少,有时,常常,总是。
将调查结果的数据进行了整理,绘制成两幅不完整的统计图如下。
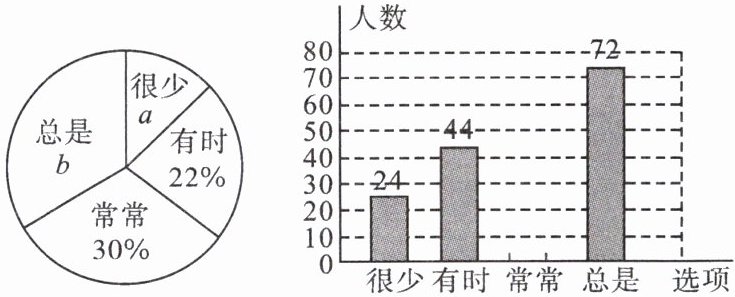
请根据图中信息,解答下列问题。
(1)该调查的样本容量为____
(2)请你补全条形统计图。
(3)若该校有3200名学生,请你估计其中“常常”和“总是”对错题进行整理、分析、改正的学生共有多少名。
____
设计问题:对自己做错的题目进行整理、分析、改正。
答案选项:很少,有时,常常,总是。
将调查结果的数据进行了整理,绘制成两幅不完整的统计图如下。

请根据图中信息,解答下列问题。
(1)该调查的样本容量为____
200
____,$a=$____12
____%,$b=$____36
____%,“常常”对应扇形的圆心角的度数为____108°
____。(2)请你补全条形统计图。
(3)若该校有3200名学生,请你估计其中“常常”和“总是”对错题进行整理、分析、改正的学生共有多少名。
____
3200×30%+3200×36%=2112(名)答:估计“常常”和“总是”对错题进行整理、分析、改正的学生共有2112名。
____
答案:
(1) 200; 12; 36; $ 108 ^ { \circ } $.
(2) 图略.
(3) $ 3200 × 30 \% + 3200 × 36 \% = 2112 $ (名).
答: 估计“常常”和“总是”对错题进行整理、分析、改正的学生共有 2112 名.
(1) 200; 12; 36; $ 108 ^ { \circ } $.
(2) 图略.
(3) $ 3200 × 30 \% + 3200 × 36 \% = 2112 $ (名).
答: 估计“常常”和“总是”对错题进行整理、分析、改正的学生共有 2112 名.
8. 如下图,在平面直角坐标系中,点$A(a,0)$,$B(0,b)$,$C(0,c)$,其中a是-64的立方根,b是-a的算术平方根,$c= \frac {1}{2}(a-b)$。
(1)求$\triangle ABC$的面积;
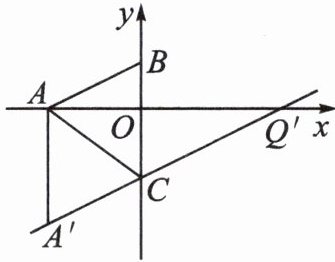
(2)点A以m个单位长度/s的速度向下运动至点$A'$,与此同时,点Q从原点出发,以2个单位长度/s的速度沿x轴向右运动至点$Q'$。若3s后,点$A'$,C,$Q'$在同一条直线上,求m的值。
(1)
(2)
(1)求$\triangle ABC$的面积;

(2)点A以m个单位长度/s的速度向下运动至点$A'$,与此同时,点Q从原点出发,以2个单位长度/s的速度沿x轴向右运动至点$Q'$。若3s后,点$A'$,C,$Q'$在同一条直线上,求m的值。
(1)
10
(2)
$\frac{5}{3}$
答案:
(1) $ a = \sqrt [ 3 ] { - 64 } = - 4 $, $ b = \sqrt { 4 } = 2 $, $ c = \frac { - 4 - 2 } { 2 } = - 3 $,
所以 $ A ( - 4,0 ) $, $ B ( 0,2 ) $, $ C ( 0, - 3 ) $.
所以 $ S _ { \triangle A B C } = \frac { 1 } { 2 } × B C × O A = \frac { 1 } { 2 } × 5 × 4 = 10 $.
(2) 由题意, 知 $ O Q ^ { \prime } = 2 × 3 = 6 $, $ A A ^ { \prime } = 3 m $.
因为点 $ A ^ { \prime } $, $ C $, $ Q ^ { \prime } $ 在同一条直线上, 所以 $ S _ { \triangle A ^ { \prime } Q ^ { \prime } A } = S _ { \triangle C Q ^ { \prime } O } + S _ { 梯形 A A ^ { \prime } C O } $.
所以 $ \frac { 1 } { 2 } × 10 × 3 m = \frac { 1 } { 2 } × 6 × 3 + \frac { 1 } { 2 } × ( 3 + 3 m ) × 4 $.
解得 $ m = \frac { 5 } { 3 } $.
(1) $ a = \sqrt [ 3 ] { - 64 } = - 4 $, $ b = \sqrt { 4 } = 2 $, $ c = \frac { - 4 - 2 } { 2 } = - 3 $,
所以 $ A ( - 4,0 ) $, $ B ( 0,2 ) $, $ C ( 0, - 3 ) $.
所以 $ S _ { \triangle A B C } = \frac { 1 } { 2 } × B C × O A = \frac { 1 } { 2 } × 5 × 4 = 10 $.
(2) 由题意, 知 $ O Q ^ { \prime } = 2 × 3 = 6 $, $ A A ^ { \prime } = 3 m $.
因为点 $ A ^ { \prime } $, $ C $, $ Q ^ { \prime } $ 在同一条直线上, 所以 $ S _ { \triangle A ^ { \prime } Q ^ { \prime } A } = S _ { \triangle C Q ^ { \prime } O } + S _ { 梯形 A A ^ { \prime } C O } $.
所以 $ \frac { 1 } { 2 } × 10 × 3 m = \frac { 1 } { 2 } × 6 × 3 + \frac { 1 } { 2 } × ( 3 + 3 m ) × 4 $.
解得 $ m = \frac { 5 } { 3 } $.
查看更多完整答案,请扫码查看


