第45页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
1. 用加减消元法将方程组$\left\{\begin{array}{l} 8x+7y= -20,\\ 8x-5y= 16\end{array} \right. 中的未知数x$消去,得到的方程是(
A.$2y= -4$
B.$12y= -36$
C.$-12y= -4$
D.$2y= 36$
B
)A.$2y= -4$
B.$12y= -36$
C.$-12y= -4$
D.$2y= 36$
答案:
1.B
2. 解方程组$\left\{\begin{array}{l} x+y= 6,\enclose{circle} {1}\\ y= 2x\enclose{circle} {2}\end{array} \right. $时,将②代入①中得到的方程是(
A.$x-2x= 6$
B.$2y+y= 6$
C.$x+2x= 6$
D.$y+y= 6$
C
)A.$x-2x= 6$
B.$2y+y= 6$
C.$x+2x= 6$
D.$y+y= 6$
答案:
2.C
3. 中国清代算书《御制数理精蕴》中有这样一题:“马四匹、牛六头,共价四十八两(‘两’为我国古代货币单位);马二匹、牛五头,共价三十八两,问马、牛各价几何?”设马每匹$x$两,牛每头$y$两,根据题意可列方程组为(
A.$\left\{\begin{array}{l} 4x+6y= 38,\\ 2x+5y= 48\end{array} \right. $
B.$\left\{\begin{array}{l} 4x+6y= 48,\\ 2x+5y= 38\end{array} \right. $
C.$\left\{\begin{array}{l} 4x+6y= 48,\\ 5x+2y= 38\end{array} \right. $
D.$\left\{\begin{array}{l} 4y+6x= 48,\\ 2x+5y= 38\end{array} \right. $
B
)A.$\left\{\begin{array}{l} 4x+6y= 38,\\ 2x+5y= 48\end{array} \right. $
B.$\left\{\begin{array}{l} 4x+6y= 48,\\ 2x+5y= 38\end{array} \right. $
C.$\left\{\begin{array}{l} 4x+6y= 48,\\ 5x+2y= 38\end{array} \right. $
D.$\left\{\begin{array}{l} 4y+6x= 48,\\ 2x+5y= 38\end{array} \right. $
答案:
3.B
4. 如下图,在周长为60的长方形$ABCD$中放入六个相同的小长方形,若$AB= 14$,则图中阴影部分的面积为(
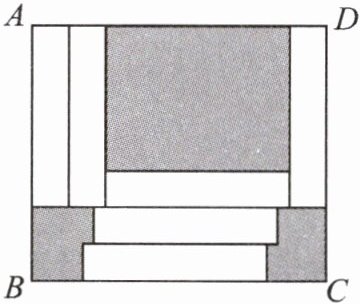
A.104
B.120
C.224
D.344
A
)
A.104
B.120
C.224
D.344
答案:
4.A
5. 方程组$\left\{\begin{array}{l} x+2y+z= 0,\\ 2x-y-z= 1,\\ 3x-y+z= 8\end{array} \right. $的解是(
A.$\left\{\begin{array}{l} x= 0,\\ y= 1,\\ z= -2\end{array} \right. $
B.$\left\{\begin{array}{l} x= 0,\\ y= 0,\\ z= 1\end{array} \right. $
C.$\left\{\begin{array}{l} x= 0,\\ y= -1,\\ z= 0\end{array} \right. $
D.$\left\{\begin{array}{l} x= 1,\\ y= -2,\\ z= 3\end{array} \right. $
D
)A.$\left\{\begin{array}{l} x= 0,\\ y= 1,\\ z= -2\end{array} \right. $
B.$\left\{\begin{array}{l} x= 0,\\ y= 0,\\ z= 1\end{array} \right. $
C.$\left\{\begin{array}{l} x= 0,\\ y= -1,\\ z= 0\end{array} \right. $
D.$\left\{\begin{array}{l} x= 1,\\ y= -2,\\ z= 3\end{array} \right. $
答案:
5.D
6. 对于实数$x$,$y$,定义新运算:$F(x,y)= mx+ny$(其中$m$,$n$均为非零常数),等式右边是实数的四则运算,例如$F(0,0)= m×0+n×0= 0$.若$F(1,-3)= 6$,$F(2,5)= 1$,则$F(3,-2)= $______
11
.
答案:
6.11
查看更多完整答案,请扫码查看


