《2025年青于蓝暑假作业七年级》

7. 如下图,C,D分别为AE,BF上的点,G为AF与CD的交点,$∠B= ∠CDF$,$∠1= ∠2$,$∠3= 64^{\circ }$.

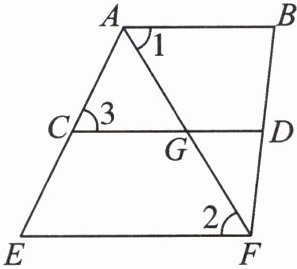
(1)求证：$CD// EF$.
证明：∵ $ ∠B = ∠CDF $，∴ $ AB // CD $。
∵ $ ∠1 = ∠2 $，∴ $ AB // EF $。∴ $ CD // EF $。
(2)若AF平分$∠BAE$,求$∠1$的度数.
$58^{\circ }$

答案： 7.
(1) 证明：
∵ $ ∠B = ∠CDF $，
∴ $ AB // CD $。
∵ $ ∠1 = ∠2 $，
∴ $ AB // EF $。
∴ $ CD // EF $。
(2)
∵ $ AB // CD $，
∴ $ ∠3 + ∠BAE = 180^\circ $。
∴ $ ∠BAE = 180^\circ - ∠3 = 180^\circ - 64^\circ = 116^\circ $。
又 $ AF $ 平分 $ ∠BAE $，
∴ $ ∠1 = \frac{116^\circ}{2} = 58^\circ $。

8. 随着“低碳生活,绿色出行”理念的普及,新能源汽车正逐渐成为人们喜爱的交通工具.某汽车4S店计划到汽车城购进一批新能源汽车进行销售.据了解,购进2辆A型新能源汽车、3辆B型新能源汽车共需80万元；购进3辆A型新能源汽车、2辆B型新能源汽车共需95万元.
(1)A,B两种型号的新能源汽车每辆进价分别为多少万元？
(2)若该4S店计划正好用180万元购进以上两种型号的新能源汽车(两种型号的汽车均购买),请设计出符合要求的所有购买方案.
(3)在问题(2)的条件下,销售1辆A型新能源汽车可获利1.2万元,销售1辆B型新能源汽车可获利0.8万元.假如这些新能源汽车全部售出,哪种方案所获利润最大？请求出最大利润.

答案： 8.
(1) 设每辆 A 型新能源汽车的进价为 $ x $ 万元，每辆 B 型新能源汽车的进价为 $ y $ 万元。
由题意，得 $ \begin{cases} 2x + 3y = 80, \\ 3x + 2y = 95. \end{cases} $ 解得 $ \begin{cases} x = 25, \\ y = 10. \end{cases} $
答：每辆 A 型新能源汽车的进价为 25 万元，每辆 B 型新能源汽车的进价为 10 万元。
(2) 设购买 A 型新能源汽车 $ a $ 辆，B 型新能源汽车 $ b $ 辆。
由题意，得 $ 25a + 10b = 180 $，则 $ b = \frac{36 - 5a}{2} $。
因为 $ a $，$ b $ 为正整数，所以 $ a $ 为偶数，且 $ 1 \leq a \leq 7 $。所以 $ a $ 的可能取值为 2，4，6。
当 $ a = 2 $ 时，$ b = 13 $。当 $ a = 4 $ 时，$ b = 8 $。
当 $ a = 6 $ 时，$ b = 3 $。
答：共有 3 种购买方案。方案一：购买 A 型新能源汽车 2 辆，B 型新能源汽车 13 辆。方案二：购买 A 型新能源汽车 4 辆，B 型新能源汽车 8 辆。方案三：购买 A 型新能源汽车 6 辆，B 型新能源汽车 3 辆。
(3) 方案一的利润为 $ 2 × 1.2 + 13 × 0.8 = 12.8 $（万元）。
方案二的利润为 $ 4 × 1.2 + 8 × 0.8 = 11.2 $（万元）。
方案三的利润为 $ 6 × 1.2 + 3 × 0.8 = 9.6 $（万元）。
因为 $ 12.8 ＞ 11.2 ＞ 9.6 $，所以方案一获得的利润最大，最大利润为 12.8 万元。
答：方案一所获利润最大，最大利润为 12.8 万元。