《2025年Happy暑假作业快乐暑假武汉大学出版社七年级数学》

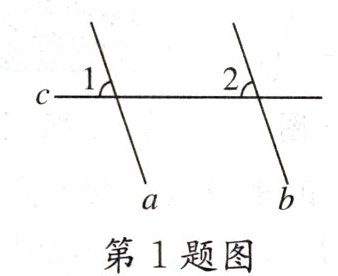
1. (★★)如图,$a// b$,a,b被c所截,得到$∠1= ∠2$的依据是 ( )


A.两直线平行,同位角相等
B.两直线平行,内错角相等
C.同位角相等,两直线平行
D.内错角相等,两直线平行

答案： 【解析】：已知直线$a// b$，直线$c$为截线。观察图形可知，$\angle1$和$\angle2$分别位于截线$c$的同侧，且在被截直线$a$、$b$的同一方，符合同位角的位置特征。因为两直线平行，同位角相等，所以由$a// b$可得出$\angle1 = \angle2$。选项C、D是由角的关系推出直线平行，与题目已知直线平行推出角相等不符；$\angle1$和$\angle2$不是内错角，故B选项错误。
【答案】：A

2. (★★)同一平面内有四条互不重合的直线a,b,c,d,若$a// b,a⊥c,b⊥d$,则直线c,d的位置关系为 ( )

A.互相垂直
B.互相平行
C.相交
D.无法确定

答案： 【解析】：在同一平面内，因为$a// b$，且$a\perp c$，根据两平行线中的一条垂直于第三条直线，另一条也垂直于第三条直线，所以$b\perp c$。又因为$b\perp d$，在同一平面内，垂直于同一条直线的两条直线互相平行，所以$c// d$。
【答案】：B

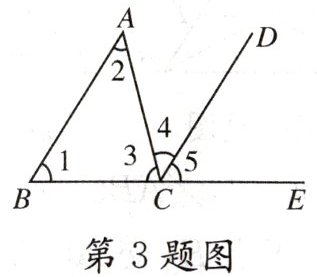
3. (★★)如图,如果$AB// CD$,那么 ( )


A.$∠1= ∠4$
B.$∠1= ∠3$
C.$∠2= ∠3$
D.$∠1= ∠5$

答案： 【解析】：因为 $AB // CD$，根据两直线平行，同位角相等，$\angle 1$ 和 $\angle 5$ 是直线 $AB$、$CD$ 被直线 $BE$ 所截形成的同位角，所以 $\angle 1 = \angle 5$。
【答案】：D

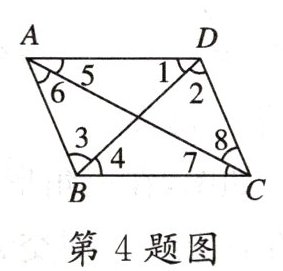
4. (★★★)如图,如果$AB// CD$,那么 ( )


A.$∠1= ∠4,∠2= ∠5$
B.$∠2= ∠3,∠4= ∠5$
C.$∠1= ∠4,∠5= ∠7$
D.$∠2= ∠3,∠6= ∠8$

答案：
∵AB//CD
∴∠2=∠3（两直线平行，内错角相等）
∠6=∠8（两直线平行，内错角相等）
∴选项D正确

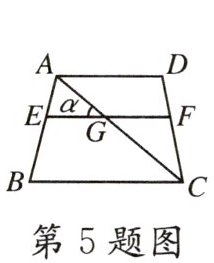
5. (★★★)如图,$AD// EF// BC$,AC平分$∠BCD$,图中和α相等的角有 ( )


A.2个
B.3个
C.4个
D.5个

答案： 【解析】：因为 $AD// EF// BC$，$AC$ 平分 $\angle BCD$，设 $\angle EGA = \alpha$。
1. 由于 $AD// EF$，根据两直线平行，内错角相等，可得 $\angle DAC=\alpha$。
2. 因为 $EF// BC$，根据两直线平行，同位角相等，可得 $\angle ACB = \alpha$。
3. 又因为 $AC$ 平分 $\angle BCD$，所以 $\angle ACB=\angle ACD$，因此 $\angle ACD=\alpha$。
4. 由于 $AD// BC$，根据两直线平行，内错角相等，可得 $\angle DAC = \angle ACB$，而 $\angle DAC=\alpha$，$\angle ACB=\alpha$，同时 $\angle ACD=\alpha$，另外，$\angle FGC$ 与 $\angle EGA$ 是对顶角，所以 $\angle FGC=\alpha$。
综上，和 $\alpha$ 相等的角有 $\angle DAC$、$\angle ACB$、$\angle ACD$、$\angle FGC$，共 4 个。
【答案】：C

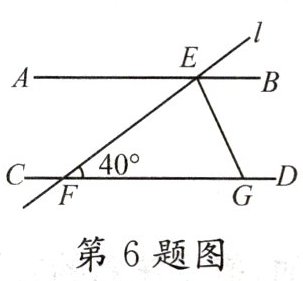
6. (★★★)如图,已知$AB// CD$,直线l分别交AB,CD于点E,F,EG平分$∠BEF$,若$∠EFG= 40^{\circ }$,则$∠EGF$的度数是 ( )


A.$60^{\circ }$
B.$70^{\circ }$
C.$80^{\circ }$
D.$90^{\circ }$

答案： 【解析】：已知$AB// CD$，直线$l$分别交$AB$，$CD$于点$E$，$F$，所以$\angle BEF$与$\angle EFG$是同旁内角，根据两直线平行，同旁内角互补，可得$\angle BEF + \angle EFG = 180^{\circ}$。
因为$\angle EFG = 40^{\circ}$，所以$\angle BEF = 180^{\circ}-\angle EFG = 180^{\circ}-40^{\circ}=140^{\circ}$。
又因为$EG$平分$\angle BEF$，所以$\angle BEG=\frac{1}{2}\angle BEF=\frac{1}{2}×140^{\circ}=70^{\circ}$。
由于$AB// CD$，$\angle EGF$与$\angle BEG$是内错角，根据两直线平行，内错角相等，可得$\angle EGF = \angle BEG = 70^{\circ}$。
【答案】：B

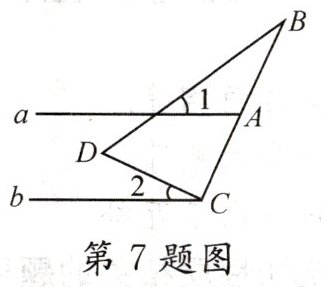
7. (★★★)如图,直线$a// b$,直角三角尺DCB按如图所示方式放置,$∠DCB= 90^{\circ }$,若$∠1+∠B= 60^{\circ }$,则$∠2$的度数为 ( )


A.$35^{\circ }$
B.$30^{\circ }$
C.$25^{\circ }$
D.$20^{\circ }$

答案： 【解析】：如图，延长BA交直线b于点E。
因为直线$a // b$，根据两直线平行，内错角相等，所以$\angle 1 = \angle BEC$。
已知$\angle 1 + \angle B = 60^\circ$，则$\angle BEC + \angle B = 60^\circ$。
在$\triangle BEC$中，根据三角形内角和定理，$\angle BCE = 180^\circ - (\angle BEC + \angle B) = 180^\circ - 60^\circ = 120^\circ$。
因为$\angle DCB = 90^\circ$，所以$\angle 2 = \angle BCE - \angle DCB = 120^\circ - 90^\circ = 30^\circ$。
【答案】：B