《2025年Happy暑假作业快乐暑假武汉大学出版社七年级数学》

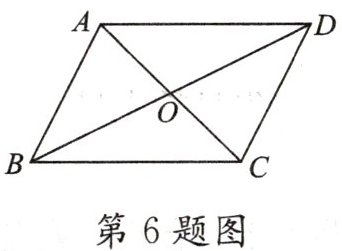
6. (★★★)如图,填空并在括号中填写推理依据:
(1)由 $ ∠ABD = ∠CDB $ 得______ $ // $______( );
(2)由 $ ∠CAD = ∠ACB $ 得______ $ // $______( );
(3)由 $ ∠CBA + ∠BAD = 180^\circ $ 得______ $ // $______( ).

答案： 【解析】：
(1) 观察图形，∠ABD 和∠CDB 是直线 AB 和 CD 被直线 BD 所截形成的内错角。因为内错角相等，两直线平行，所以当∠ABD = ∠CDB 时，AB // CD。
(2) ∠CAD 和∠ACB 是直线 AD 和 BC 被直线 AC 所截形成的内错角。依据内错角相等，两直线平行，当∠CAD = ∠ACB 时，AD // BC。
(3) ∠CBA 和∠BAD 是直线 AD 和 BC 被直线 AB 所截形成的同旁内角。由于同旁内角互补，两直线平行，当∠CBA + ∠BAD = 180°时，AD // BC。
【答案】：
(1)AB，CD，内错角相等，两直线平行；
(2)AD，BC，内错角相等，两直线平行；
(3)AD，BC，同旁内角互补，两直线平行

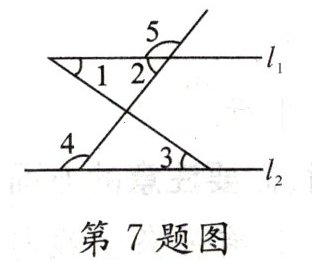
7. (★★★)如图,尽可能多地写出能判定直线 $ l_1 // l_2 $ 的条件:
______.

答案： 【解析】：要判定直线 $ l_1 // l_2 $，可依据平行线的判定定理，结合图中角的位置关系进行分析：
1. 同位角相等，两直线平行：$∠1$ 与 $∠3$ 是同位角，若 $∠1 = ∠3$，则 $ l_1 // l_2 $。
2. 内错角相等，两直线平行：$∠2$ 与 $∠3$ 是内错角，若 $∠2 = ∠3$，则 $ l_1 // l_2 $。
3. 同旁内角互补，两直线平行：$∠2$ 与 $∠4$ 是同旁内角，若 $∠2 + ∠4 = 180^\circ$，则 $ l_1 // l_2 $；$∠1$ 与 $∠4$ 是同位角的邻补角关系，若 $∠1 + ∠4 = 180^\circ$，也可推出同旁内角互补（此处需结合对顶角等性质进一步验证，实际图中 $∠5$ 与 $∠1$ 是对顶角，$∠5$ 与 $∠4$ 是同旁内角，所以 $∠5 + ∠4 = 180^\circ$ 即 $∠1 + ∠4 = 180^\circ$ 时，$ l_1 // l_2 $）。
4. 对顶角转化：$∠5$ 与 $∠1$ 是对顶角，所以 $∠5 = ∠1$，若 $∠5 = ∠3$（同位角），则等价于 $∠1 = ∠3$；若 $∠5 + ∠4 = 180^\circ$（同旁内角），等价于 $∠1 + ∠4 = 180^\circ$。
综上，可判定 $ l_1 // l_2 $ 的条件有：$∠1 = ∠3$，$∠2 = ∠3$，$∠2 + ∠4 = 180^\circ$，$∠1 + ∠4 = 180^\circ$，$∠5 = ∠3$，$∠5 + ∠4 = 180^\circ$ 等，其中最直接且不重复的核心条件为 $∠1 = ∠3$，$∠2 = ∠3$，$∠2 + ∠4 = 180^\circ$，$∠1 + ∠4 = 180^\circ$。
【答案】：$∠1 = ∠3$，$∠2 = ∠3$，$∠2 + ∠4 = 180^\circ$，$∠1 + ∠4 = 180^\circ$

8. (★★★)如图,尽可能多地写出能判定 $ AB // CD $ 的条件:
______.

答案： $∠1=∠4$，$∠2=∠5$，$∠BAD+∠ADC=180°$，$∠ABC+∠BCD=180°$，$∠BAC=∠ACD$

9. (★★★)如图,已知 $ ∠A = ∠ACE, ∠B = ∠BDF $,且 $ ∠A = ∠B $. 求证: $ EC // DF $.

答案： 证明：
∵∠A=∠ACE，∠B=∠BDF，∠A=∠B
∴∠ACE=∠BDF
∵∠ACE=∠BCD
∴∠BCD=∠BDF
∴EC//DF（内错角相等，两直线平行）

10. (★★★)如图, $ AE $ 是 $ ∠BAP $ 的平分线, $ PE $ 是 $ ∠APD $ 的平分线, $ ∠2 + ∠3 = 90^\circ $. 求证: $ AB // CD $.

答案： 证明：
∵AE是∠BAP的平分线
∴∠1=∠2（角平分线的定义）
∵PE是∠APD的平分线
∴∠3=∠4（角平分线的定义）
∵∠2+∠3=90°
∴∠1+∠2+∠3+∠4=180°
即∠BAP+∠APD=180°
∴AB//CD（同旁内角互补，两直线平行）