《2025年Happy暑假作业快乐暑假武汉大学出版社七年级数学》

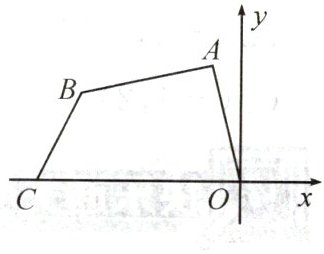
16. (★★★)如图,四边形ABCO各个顶点的坐标分别为$A(-2,8)$,$B(-11,6)$,$C(-14,0)$,$O(0,0)$。试求这个四边形的面积。

答案： 解：过点A作AD⊥x轴于点D，过点B作BE⊥x轴于点E，
∵A(-2,8)，B(-11,6)，C(-14,0)，O(0,0)，
∴OD=2，AD=8，OE=11，BE=6，OC=14，
DE=OE-OD=11-2=9，
CE=OC-OE=14-11=3，
S四边形ABCO=S梯形ABED+S△BEC+S△AOD，
S梯形ABED=$\frac{1}{2}$×(BE+AD)×DE=$\frac{1}{2}$×(6+8)×9=63，
S△BEC=$\frac{1}{2}$×CE×BE=$\frac{1}{2}$×3×6=9，
S△AOD=$\frac{1}{2}$×OD×AD=$\frac{1}{2}$×2×8=8，
∴S四边形ABCO=63+9+8=80.

17. (★★★★)如图,在平面直角坐标系中：
(1)描出下列各点$A(-2,3)$,$B(-4,-2)$,$C(1,-2)$；
(2)若以点A,B,C为顶点,作一个平行四边形,试写出第四个顶点的坐标；
(3)求这个平行四边形的面积。

答案： 【解析】：
(1) 在平面直角坐标系中，分别找到横坐标与纵坐标对应的位置，即可描出点$A(-2,3)$、$B(-4,-2)$、$C(1,-2)$。
(2) 设第四个顶点为$D(x,y)$。
当$AB$为平行四边形的一条边，$AC$为另一条边时，根据平行四边形对边平行且相等，可得$\overrightarrow{AB}=\overrightarrow{DC}$。$\overrightarrow{AB}=(-4 - (-2), -2 - 3)=(-2,-5)$，$\overrightarrow{DC}=(1 - x, -2 - y)$，则$\begin{cases}1 - x=-2\\-2 - y=-5\end{cases}$，解得$\begin{cases}x=3\\y=3\end{cases}$，即$D(3,3)$。
当$AB$为平行四边形的一条边，$BC$为另一条边时，$\overrightarrow{AB}=\overrightarrow{CD}$。$\overrightarrow{BC}=(1 - (-4), -2 - (-2))=(5,0)$，$\overrightarrow{AD}=(x - (-2), y - 3)=(x + 2,y - 3)$，$\overrightarrow{BC}=\overrightarrow{AD}$，则$\begin{cases}x + 2=5\\y - 3=0\end{cases}$，解得$\begin{cases}x=3\\y=3\end{cases}$（与上述情况重复，舍去）。或$\overrightarrow{AC}=\overrightarrow{BD}$，$\overrightarrow{AC}=(1 - (-2), -2 - 3)=(3,-5)$，$\overrightarrow{BD}=(x - (-4), y - (-2))=(x + 4,y + 2)$，则$\begin{cases}x + 4=3\\y + 2=-5\end{cases}$，解得$\begin{cases}x=-1\\y=-7\end{cases}$，即$D(-1,-7)$。
当$AC$和$BC$为平行四边形的两条边时，$\overrightarrow{AC}=\overrightarrow{BD}$，$\overrightarrow{BC}=\overrightarrow{AD}$，$\overrightarrow{AB}=\overrightarrow{CD}$另一种情况：$\overrightarrow{BA}=\overrightarrow{CD}$，$\overrightarrow{BA}=(-2 - (-4), 3 - (-2))=(2,5)$，$\overrightarrow{CD}=(x - 1,y - (-2))=(x - 1,y + 2)$，则$\begin{cases}x - 1=2\\y + 2=5\end{cases}$，解得$\begin{cases}x=3\\y=3\end{cases}$（重复）。或$\overrightarrow{BC}=\overrightarrow{DA}$，$\overrightarrow{BC}=(5,0)$，$\overrightarrow{DA}=(-2 - x,3 - y)$，则$\begin{cases}-2 - x=5\\3 - y=0\end{cases}$，解得$\begin{cases}x=-7\\y=3\end{cases}$，即$D(-7,3)$。
综上，第四个顶点的坐标为$(3,3)$或$(-1,-7)$或$(-7,3)$。
(3) 由点$B(-4,-2)$、$C(1,-2)$可知，$BC$在直线$y=-2$上，$BC$的长度为$1 - (-4)=5$。点$A$到$BC$的距离为$3 - (-2)=5$，所以平行四边形的面积为$BC×$距离$=5×5=25$。
【答案】：
(2)$(3,3)$或$(-1,-7)$或$(-7,3)$；
(3)$25$

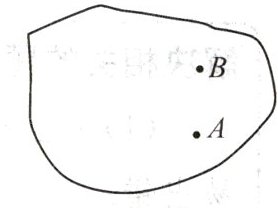
如图为某废墟示意图,由于雨水冲蚀,残缺不全,依稀可见钟楼坐标为$A(5,-2)$,街口坐标为$B(5,2)$,资料记载阿明先生的祖居的坐标为$(2,1)$,你能帮助阿明先生找到他家的老屋吗？

答案： 1. 首先，根据已知点确定坐标系：
已知$A(5, - 2)$，$B(5,2)$，可知$A$、$B$两点横坐标相同，$AB$垂直于$x$轴。
计算$AB$的距离：根据两点间距离公式$d=\vert y_2 - y_1\vert$（当$x_1 = x_2$时），$AB=\vert2-(-2)\vert=\vert2 + 2\vert = 4$。
以$AB$的垂直平分线为$x$轴（因为$AB$中点的纵坐标$y=\frac{-2 + 2}{2}=0$），过$A$（或$B$）点垂直于$AB$的直线为$y$轴（$x = 5$）建立平面直角坐标系。
2. 然后，根据坐标确定祖居位置：
已知祖居坐标为$(2,1)$。
在建立好的平面直角坐标系中，先在$x$轴上找到$x = 2$的点，再在$y$轴上找到$y = 1$的点，过$x = 2$作$y$轴的平行线，过$y = 1$作$x$轴的平行线，两线交点即为祖居$(2,1)$的位置。
所以，在建立以$AB$垂直平分线为$x$轴，过$A$（或$B$）垂直于$AB$的直线为$y$轴的平面直角坐标系后，根据坐标$(2,1)$可找到阿明先生家老屋。