12 (★★★)已知 $ \begin{cases} x = 2, \\ y = -1 \end{cases} $ 是方程组 $ \begin{cases} mx - y = 3, \\ x - ny = 6 \end{cases} $ 的解,则 $ m = $____,$ n = $____.
答案:
【解析】:因为$\begin{cases} x = 2 \\ y = -1 \end{cases}$是方程组$\begin{cases} mx - y = 3 \\ x - ny = 6 \end{cases}$的解,所以将$x = 2$,$y = -1$代入方程组中。
对于第一个方程$mx - y = 3$,代入可得:$2m - (-1) = 3$,即$2m + 1 = 3$,$2m = 3 - 1$,$2m = 2$,解得$m = 1$。
对于第二个方程$x - ny = 6$,代入可得:$2 - n×(-1) = 6$,即$2 + n = 6$,$n = 6 - 2$,解得$n = 4$。
【答案】:1,4
对于第一个方程$mx - y = 3$,代入可得:$2m - (-1) = 3$,即$2m + 1 = 3$,$2m = 3 - 1$,$2m = 2$,解得$m = 1$。
对于第二个方程$x - ny = 6$,代入可得:$2 - n×(-1) = 6$,即$2 + n = 6$,$n = 6 - 2$,解得$n = 4$。
【答案】:1,4
13. (★★★)根据题意设元列出方程组(不需要解方程组):
(1)明明到邮局买 0.8 元与 2 元的邮票共 13 枚,共花去 20 元钱,问明明两种邮票各买了多少枚?
(2)将若干只鸡放入若干个笼中,若每个笼中放 4 只,则有一只鸡无笼可放;若每个笼中放 5 只,则恰有一笼无鸡可放,问有多少只鸡、多少个笼?
(1)明明到邮局买 0.8 元与 2 元的邮票共 13 枚,共花去 20 元钱,问明明两种邮票各买了多少枚?
(2)将若干只鸡放入若干个笼中,若每个笼中放 4 只,则有一只鸡无笼可放;若每个笼中放 5 只,则恰有一笼无鸡可放,问有多少只鸡、多少个笼?
答案:
【解析】:
(1)设明明买了0.8元的邮票$x$枚,2元的邮票$y$枚。根据邮票总数为13枚可列方程$x + y = 13$;根据共花去20元可列方程$0.8x + 2y = 20$,从而得到方程组。
(2)设有$x$只鸡,$y$个笼。每个笼放4只时,有一只鸡无笼可放,可列方程$4y + 1 = x$;每个笼放5只时,恰有一笼无鸡,即有$(y - 1)$个笼有鸡,可列方程$5(y - 1) = x$,进而得到方程组。
【答案】:
(1)$\begin{cases}x + y = 13 \\ 0.8x + 2y = 20\end{cases}$;
(2)$\begin{cases}4y + 1 = x \\ 5(y - 1) = x\end{cases}$
(1)设明明买了0.8元的邮票$x$枚,2元的邮票$y$枚。根据邮票总数为13枚可列方程$x + y = 13$;根据共花去20元可列方程$0.8x + 2y = 20$,从而得到方程组。
(2)设有$x$只鸡,$y$个笼。每个笼放4只时,有一只鸡无笼可放,可列方程$4y + 1 = x$;每个笼放5只时,恰有一笼无鸡,即有$(y - 1)$个笼有鸡,可列方程$5(y - 1) = x$,进而得到方程组。
【答案】:
(1)$\begin{cases}x + y = 13 \\ 0.8x + 2y = 20\end{cases}$;
(2)$\begin{cases}4y + 1 = x \\ 5(y - 1) = x\end{cases}$
14. (★★★★)在解方程组 $ \begin{cases} cx - 3y = 5, \\ ax + by = 2 \end{cases} $ 时,小强得到的正确解为 $ \begin{cases} y = 2, \\ x = 1, \end{cases} $ 小明由于看错了方程组中的 $ c $ 得到方程组的解为 $ \begin{cases} y = 1, \\ x = -3, \end{cases} $ 试求方程组中的 $ a,b,c $ 的值.
答案:
解:将$\begin{cases} x = 1 \\ y = 2 \end{cases}$代入$cx - 3y = 5$,
得$c×1 - 3×2 = 5$,
$c - 6 = 5$,
$c = 11$。
将$\begin{cases} x = 1 \\ y = 2 \end{cases}$和$\begin{cases} x = -3 \\ y = 1 \end{cases}$分别代入$ax + by = 2$,
得$\begin{cases} a + 2b = 2 \\ -3a + b = 2 \end{cases}$。
由$-3a + b = 2$得$b = 3a + 2$,
将$b = 3a + 2$代入$a + 2b = 2$,
$a + 2(3a + 2) = 2$,
$a + 6a + 4 = 2$,
$7a = -2$,
$a = -\dfrac{2}{7}$。
将$a = -\dfrac{2}{7}$代入$b = 3a + 2$,
$b = 3×(-\dfrac{2}{7}) + 2 = -\dfrac{6}{7} + \dfrac{14}{7} = \dfrac{8}{7}$。
所以$a = -\dfrac{2}{7}$,$b = \dfrac{8}{7}$,$c = 11$。
得$c×1 - 3×2 = 5$,
$c - 6 = 5$,
$c = 11$。
将$\begin{cases} x = 1 \\ y = 2 \end{cases}$和$\begin{cases} x = -3 \\ y = 1 \end{cases}$分别代入$ax + by = 2$,
得$\begin{cases} a + 2b = 2 \\ -3a + b = 2 \end{cases}$。
由$-3a + b = 2$得$b = 3a + 2$,
将$b = 3a + 2$代入$a + 2b = 2$,
$a + 2(3a + 2) = 2$,
$a + 6a + 4 = 2$,
$7a = -2$,
$a = -\dfrac{2}{7}$。
将$a = -\dfrac{2}{7}$代入$b = 3a + 2$,
$b = 3×(-\dfrac{2}{7}) + 2 = -\dfrac{6}{7} + \dfrac{14}{7} = \dfrac{8}{7}$。
所以$a = -\dfrac{2}{7}$,$b = \dfrac{8}{7}$,$c = 11$。
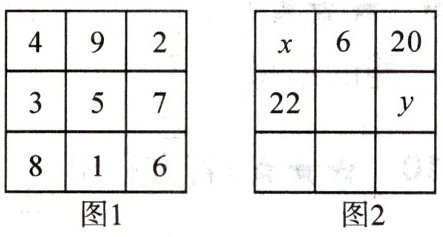
幻方是古老的数学问题,我国古代的《洛书》中记载了最早的幻方——九宫格. 将 9 个数填入幻方的空格中,要求每一横行、每一竖列以及两条对角线上的 3 个数之和相等,例如图 1 就是一个幻方,图 2 是一个未完成的幻方,你知道 $ x $ 与 $ y $ 的和吗?

答案:
【解析】:设幻方中心的数为 $ a $,幻和为 $ S $(即每一横行、竖列、对角线的和)。
在图2中,第一行的和为 $ x + 6 + 20 = S $,即 $ x = S - 26 $ ①。
第二列有数字6和$ a $,设第二列最下方的数为 $ b $,则 $ 6 + a + b = S $,即 $ b = S - a - 6 $ ②。
第一列有数字$ x $和22,设第一列最下方的数为 $ c $,则 $ x + 22 + c = S $,将①代入得 $ (S - 26) + 22 + c = S $,化简得 $ c = 4 $ ③。
第三列有数字20和$ y $,设第三列最上方的数已给出为20,中间为$ a $(对角线方向),右下角的数为 $ d $,则 $ 20 + a + d = S $(对角线),且 $ y + d + 20 = S $(第三列),可得 $ y = a $ ④(此处通过对角线和列的关系推导,实际更简便的是利用三阶幻方性质:幻和 $ S = 3a $,中心数为幻和的三分之一)。
利用第一行和主对角线(假设主对角线为左上角到右下角,即 $ x + a + d = S $,但结合第三列 $ 20 + a + d = S $,可得 $ x = 20 $?不,此处应重新用标准方法:设第二行中间数为 $ a $,则第二行和为 $ 22 + a + y = S $,第三行和为 $ c + b + d = S $($ c = 4 $ 已得)。
正确步骤:设幻和 $ S = 3a $(中心数 $ a $),则第二行:$ 22 + a + y = 3a \Rightarrow y = 2a - 22 $ ⑤。
第一行:$ x + 6 + 20 = 3a \Rightarrow x = 3a - 26 $ ⑥。
第一列:$ x + 22 + 4 = 3a $($ c = 4 $),将⑥代入:$ 3a - 26 + 22 + 4 = 3a \Rightarrow 3a = 3a $,恒成立,无法直接求 $ a $。
换用副对角线(右上角20,中心 $ a $,左下角4):$ 20 + a + 4 = 3a \Rightarrow 24 = 2a \Rightarrow a = 12 $ ⑦(关键!副对角线三个数之和为幻和,即右上角20、中心 $ a $、左下角4,它们的和是 $ S = 3a $)。
由⑦得 $ a = 12 $,则 $ S = 3×12 = 36 $。
由⑥:$ x = 3×12 - 26 = 36 - 26 = 10 $。
由⑤:$ y = 2×12 - 22 = 24 - 22 = 2 $。
所以 $ x + y = 10 + 2 = 12 $。
【答案】:12
在图2中,第一行的和为 $ x + 6 + 20 = S $,即 $ x = S - 26 $ ①。
第二列有数字6和$ a $,设第二列最下方的数为 $ b $,则 $ 6 + a + b = S $,即 $ b = S - a - 6 $ ②。
第一列有数字$ x $和22,设第一列最下方的数为 $ c $,则 $ x + 22 + c = S $,将①代入得 $ (S - 26) + 22 + c = S $,化简得 $ c = 4 $ ③。
第三列有数字20和$ y $,设第三列最上方的数已给出为20,中间为$ a $(对角线方向),右下角的数为 $ d $,则 $ 20 + a + d = S $(对角线),且 $ y + d + 20 = S $(第三列),可得 $ y = a $ ④(此处通过对角线和列的关系推导,实际更简便的是利用三阶幻方性质:幻和 $ S = 3a $,中心数为幻和的三分之一)。
利用第一行和主对角线(假设主对角线为左上角到右下角,即 $ x + a + d = S $,但结合第三列 $ 20 + a + d = S $,可得 $ x = 20 $?不,此处应重新用标准方法:设第二行中间数为 $ a $,则第二行和为 $ 22 + a + y = S $,第三行和为 $ c + b + d = S $($ c = 4 $ 已得)。
正确步骤:设幻和 $ S = 3a $(中心数 $ a $),则第二行:$ 22 + a + y = 3a \Rightarrow y = 2a - 22 $ ⑤。
第一行:$ x + 6 + 20 = 3a \Rightarrow x = 3a - 26 $ ⑥。
第一列:$ x + 22 + 4 = 3a $($ c = 4 $),将⑥代入:$ 3a - 26 + 22 + 4 = 3a \Rightarrow 3a = 3a $,恒成立,无法直接求 $ a $。
换用副对角线(右上角20,中心 $ a $,左下角4):$ 20 + a + 4 = 3a \Rightarrow 24 = 2a \Rightarrow a = 12 $ ⑦(关键!副对角线三个数之和为幻和,即右上角20、中心 $ a $、左下角4,它们的和是 $ S = 3a $)。
由⑦得 $ a = 12 $,则 $ S = 3×12 = 36 $。
由⑥:$ x = 3×12 - 26 = 36 - 26 = 10 $。
由⑤:$ y = 2×12 - 22 = 24 - 22 = 2 $。
所以 $ x + y = 10 + 2 = 12 $。
【答案】:12
查看更多完整答案,请扫码查看


