8. (★★★)如图,(1)$∠1与∠2$是____被____截成的____角;
(2)$∠2与∠3$是____被____截成的____角;
(3)$∠3与∠A$是____被____截成的____角;
(4)AB,AC 被 BE 截成的内错角是____,同旁内角是____;
(5)DE,BC 被 AB 截成的同位角是____,同旁内角是____.

(2)$∠2与∠3$是____被____截成的____角;
(3)$∠3与∠A$是____被____截成的____角;
(4)AB,AC 被 BE 截成的内错角是____,同旁内角是____;
(5)DE,BC 被 AB 截成的同位角是____,同旁内角是____.

答案:
【解析】:(1)观察图形,∠1和∠2,∠1在直线DE和BE的交点处,∠2在直线BC和BE的交点处,直线DE和BC被直线BE所截,∠1和∠2都在截线BE的同侧,且在被截线DE、BC的下方,所以是同位角。
(2)∠2与∠3,∠2在直线BC和BE的交点,∠3在直线AC和BE的交点,直线BC和AC被直线BE所截,∠2和∠3在截线BE的两侧,且在被截线BC、AC之间,所以是内错角。
(3)∠3与∠A,∠3在直线AC和BE的交点,∠A在直线AB和AC的交点,直线BE和AB被直线AC所截,∠3和∠A在截线AC的同侧,且在被截线BE、AB之间,所以是同旁内角。
(4)AB、AC被BE截,AB与BE相交形成∠ABE,AC与BE相交形成∠3,内错角是在截线两侧,被截线之间,所以∠ABE和∠3是内错角;同旁内角是在截线同侧,被截线之间,AB与BE形成的另一个角和AC与BE形成的角,即∠CBE和∠3是同旁内角(这里∠ABE和∠CBE互为邻补角,根据图形标注∠2是∠CBE,所以同旁内角是∠2和∠3)。
(5)DE、BC被AB截,DE与AB相交形成∠ADE,BC与AB相交形成∠B,同位角是在截线同侧,被截线同方向,所以∠ADE和∠B是同位角;同旁内角是在截线同侧,被截线之间,DE与AB形成的∠BDE和BC与AB形成的∠B在截线AB同侧,被截线DE、BC之间,所以∠BDE和∠B是同旁内角。
【答案】:(1)DE、BC;BE;同位;(2)BC、AC;BE;内错;(3)BE、AB;AC;同旁内;(4)∠ABE和∠3;∠2和∠3;(5)∠ADE和∠B;∠BDE和∠B
(2)∠2与∠3,∠2在直线BC和BE的交点,∠3在直线AC和BE的交点,直线BC和AC被直线BE所截,∠2和∠3在截线BE的两侧,且在被截线BC、AC之间,所以是内错角。
(3)∠3与∠A,∠3在直线AC和BE的交点,∠A在直线AB和AC的交点,直线BE和AB被直线AC所截,∠3和∠A在截线AC的同侧,且在被截线BE、AB之间,所以是同旁内角。
(4)AB、AC被BE截,AB与BE相交形成∠ABE,AC与BE相交形成∠3,内错角是在截线两侧,被截线之间,所以∠ABE和∠3是内错角;同旁内角是在截线同侧,被截线之间,AB与BE形成的另一个角和AC与BE形成的角,即∠CBE和∠3是同旁内角(这里∠ABE和∠CBE互为邻补角,根据图形标注∠2是∠CBE,所以同旁内角是∠2和∠3)。
(5)DE、BC被AB截,DE与AB相交形成∠ADE,BC与AB相交形成∠B,同位角是在截线同侧,被截线同方向,所以∠ADE和∠B是同位角;同旁内角是在截线同侧,被截线之间,DE与AB形成的∠BDE和BC与AB形成的∠B在截线AB同侧,被截线DE、BC之间,所以∠BDE和∠B是同旁内角。
【答案】:(1)DE、BC;BE;同位;(2)BC、AC;BE;内错;(3)BE、AB;AC;同旁内;(4)∠ABE和∠3;∠2和∠3;(5)∠ADE和∠B;∠BDE和∠B
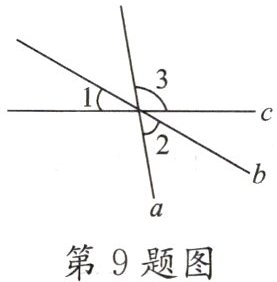
9. (★★★)如图,直线 a,b,c 交于一点,$∠1= 30^{\circ },∠2= 50^{\circ }$,则$∠3= $____.

答案:
【解析】:由图可知,直线a,b,c交于一点,形成了一个周角。周角的度数为$360^{\circ}$,$∠1$、$∠2$与$∠3$所在的角以及$∠1$的对顶角、$∠2$的对顶角共同组成了这个周角。但观察图形可发现,$∠1$、$∠2$和$∠3$所在的三个角正好是周角中不重叠的三个部分,且$∠1$的对顶角与$∠1$相等,$∠2$的对顶角与$∠2$相等,不过这里更简便的是,$∠1$、$∠2$和$∠3$所在的角以及它们各自的对顶角之和为$360^{\circ}$,而$∠3$的对顶角就是$∠3$本身,所以$2∠1 + 2∠2 + 2∠3 = 360^{\circ}$,等式两边同时除以2可得$∠1 + ∠2 + ∠3 = 180^{\circ}$。已知$∠1 = 30^{\circ}$,$∠2 = 50^{\circ}$,则$∠3=180^{\circ}-∠1 - ∠2=180^{\circ}-30^{\circ}-50^{\circ}=100^{\circ}$。
【答案】:100°
【答案】:100°
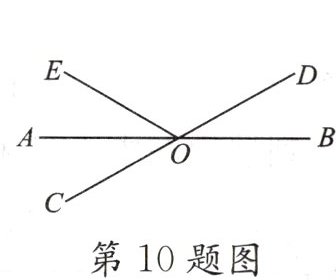
10. (★★★)如图,直线 AB,CD 交于点 O,OA 平分$∠EOC$,且$∠EOD= 120^{\circ }$,则$∠BOD= $____.

答案:
【解析】:因为直线CD上的点O,所以∠EOC与∠EOD互为邻补角,即∠EOC + ∠EOD = 180°。已知∠EOD = 120°,则∠EOC = 180° - 120° = 60°。
由于OA平分∠EOC,所以∠AOE = ∠AOC = ∠EOC / 2 = 60° / 2 = 30°。
直线AB和CD相交于点O,∠AOC与∠BOD是对顶角,根据对顶角相等的性质,可得∠BOD = ∠AOC = 30°。
【答案】:30°
由于OA平分∠EOC,所以∠AOE = ∠AOC = ∠EOC / 2 = 60° / 2 = 30°。
直线AB和CD相交于点O,∠AOC与∠BOD是对顶角,根据对顶角相等的性质,可得∠BOD = ∠AOC = 30°。
【答案】:30°
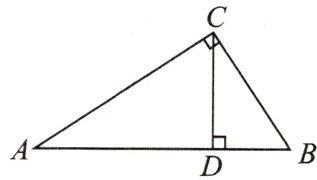
11. (★★★)如图,在三角形 ABC 中,$AC⊥BC,CD⊥AB$于点 D.
(1)AB,AC,CD 之间的大小关系为____;(用“<”号连接起来)
(2)若$AC= 12,BC= 5,AB= 13$,求点 C 到线段 AB 的距离.
(1)AB,AC,CD 之间的大小关系为____;(用“<”号连接起来)
(2)若$AC= 12,BC= 5,AB= 13$,求点 C 到线段 AB 的距离.

答案:
【解析】:(1)在直角三角形 $ABC$ 中,$AC \perp BC$,$CD \perp AB$。因为从直线外一点到这条直线所作的垂线段最短,所以 $CD$ 是点 $C$ 到 $AB$ 的垂线段,$AC$ 是直角边,$AB$ 是斜边。在直角三角形中斜边最长,所以 $AB > AC$,又因为垂线段最短,所以 $CD < AC$,因此 $CD < AC < AB$。
(2)已知 $AC = 12$,$BC = 5$,$AB = 13$。三角形 $ABC$ 的面积可以用两直角边乘积的一半计算,即 $S = \frac{1}{2} × AC × BC = \frac{1}{2} × 12 × 5 = 30$。也可以用斜边 $AB$ 乘以斜边上的高 $CD$ 的一半来计算,即 $S = \frac{1}{2} × AB × CD$。所以 $\frac{1}{2} × 13 × CD = 30$,解得 $CD = \frac{60}{13}$。
【答案】:(1)$CD < AC < AB$;(2)$\frac{60}{13}$
(2)已知 $AC = 12$,$BC = 5$,$AB = 13$。三角形 $ABC$ 的面积可以用两直角边乘积的一半计算,即 $S = \frac{1}{2} × AC × BC = \frac{1}{2} × 12 × 5 = 30$。也可以用斜边 $AB$ 乘以斜边上的高 $CD$ 的一半来计算,即 $S = \frac{1}{2} × AB × CD$。所以 $\frac{1}{2} × 13 × CD = 30$,解得 $CD = \frac{60}{13}$。
【答案】:(1)$CD < AC < AB$;(2)$\frac{60}{13}$
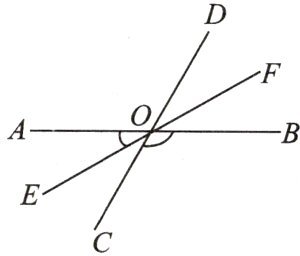
12. (★★★★)如图,直线 AB,CD 交于点 O,$∠AOE= 30^{\circ },$$∠BOC= 2∠AOC$,求$∠DOF$的度数.

答案:
∵直线AB,CD交于点O,
∴∠AOC+∠BOC=180°(邻补角互补),
∵∠BOC=2∠AOC,
∴∠AOC+2∠AOC=180°,
∴∠AOC=60°,
∵∠AOE=30°,
∴∠EOC=∠AOC-∠AOE=60°-30°=30°,
∵∠DOF与∠EOC是对顶角,
∴∠DOF=∠EOC=30°(对顶角相等)。
∵直线AB,CD交于点O,
∴∠AOC+∠BOC=180°(邻补角互补),
∵∠BOC=2∠AOC,
∴∠AOC+2∠AOC=180°,
∴∠AOC=60°,
∵∠AOE=30°,
∴∠EOC=∠AOC-∠AOE=60°-30°=30°,
∵∠DOF与∠EOC是对顶角,
∴∠DOF=∠EOC=30°(对顶角相等)。
查看更多完整答案,请扫码查看


