1. (★★)下列计算正确的是 ( )
A.$\sqrt {3}+\sqrt {2}= \sqrt {6}$
B.$3+2\sqrt {3}= 5\sqrt {3}$
C.$\sqrt {3}a-\sqrt {2}a= a$
D.$\sqrt {2}+\frac {1}{2}\sqrt {2}= \frac {3}{2}\sqrt {2}$
A.$\sqrt {3}+\sqrt {2}= \sqrt {6}$
B.$3+2\sqrt {3}= 5\sqrt {3}$
C.$\sqrt {3}a-\sqrt {2}a= a$
D.$\sqrt {2}+\frac {1}{2}\sqrt {2}= \frac {3}{2}\sqrt {2}$
答案:
【解析】:选项A,$\sqrt{3}$与$\sqrt{2}$不是同类二次根式,不能直接相加,所以A错误;选项B,3是有理数,$2\sqrt{3}$是无理数,不能合并,所以B错误;选项C,$\sqrt{3}a$与$\sqrt{2}a$不是同类二次根式,不能直接相减,所以C错误;选项D,$\sqrt{2}+\frac{1}{2}\sqrt{2}=(1+\frac{1}{2})\sqrt{2}=\frac{3}{2}\sqrt{2}$,所以D正确。
【答案】:D
【答案】:D
2. (★★)$-\frac {5}{3},-\sqrt {2},-\sqrt {3},-\frac {π}{2}$四个数中,最大的数是 ( )
A.$-\frac {5}{3}$
B.$-\sqrt {2}$
C.$-\sqrt {3}$
D.$-\frac {π}{2}$
A.$-\frac {5}{3}$
B.$-\sqrt {2}$
C.$-\sqrt {3}$
D.$-\frac {π}{2}$
答案:
【解析】:要比较$-\frac{5}{3}$,$-\sqrt{2}$,$-\sqrt{3}$,$-\frac{\pi}{2}$这四个负数的大小,根据“两个负数比较大小,绝对值大的反而小”的原则,先求出它们的绝对值并比较大小。
$\left|-\frac{5}{3}\right|=\frac{5}{3}\approx1.6667$;$\left|-\sqrt{2}\right|=\sqrt{2}\approx1.4142$;$\left|-\sqrt{3}\right|=\sqrt{3}\approx1.7321$;$\left|-\frac{\pi}{2}\right|=\frac{\pi}{2}\approx1.5708$。
比较绝对值大小:$\sqrt{3}\approx1.7321>\frac{5}{3}\approx1.6667>\frac{\pi}{2}\approx1.5708>\sqrt{2}\approx1.4142$。
所以原负数的大小关系为:$-\sqrt{2}>-\frac{\pi}{2}>-\frac{5}{3}>-\sqrt{3}$,最大的数是$-\sqrt{2}$。
【答案】:B
$\left|-\frac{5}{3}\right|=\frac{5}{3}\approx1.6667$;$\left|-\sqrt{2}\right|=\sqrt{2}\approx1.4142$;$\left|-\sqrt{3}\right|=\sqrt{3}\approx1.7321$;$\left|-\frac{\pi}{2}\right|=\frac{\pi}{2}\approx1.5708$。
比较绝对值大小:$\sqrt{3}\approx1.7321>\frac{5}{3}\approx1.6667>\frac{\pi}{2}\approx1.5708>\sqrt{2}\approx1.4142$。
所以原负数的大小关系为:$-\sqrt{2}>-\frac{\pi}{2}>-\frac{5}{3}>-\sqrt{3}$,最大的数是$-\sqrt{2}$。
【答案】:B
3. (★★★)如图,数轴上表示$1,\sqrt {3}$的对应点分别为点A,点B.若点B关于点A的对称点为点C,则点C所表示的数为 ( )
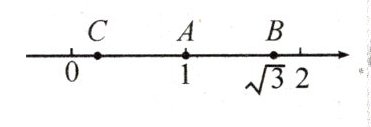
A.$\sqrt {3}-1$
B.$1-\sqrt {3}$
C.$2-\sqrt {3}$
D.$\sqrt {3}-2$
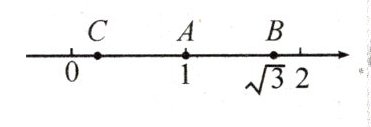
A.$\sqrt {3}-1$
B.$1-\sqrt {3}$
C.$2-\sqrt {3}$
D.$\sqrt {3}-2$
答案:
【解析】:设点C所表示的数为$x$。因为点B关于点A的对称点为点C,所以点A是线段BC的中点。根据中点坐标公式,中点所表示的数等于两端点所表示数的和的一半,可得$1 = \frac{x + \sqrt{3}}{2}$。解方程可得$x = 2 - \sqrt{3}$。
【答案】:C
【答案】:C
4. (★★)写出在3和4之间的一个无理数______.
答案:
【解析】:无理数是指无限不循环小数。要找到3和4之间的无理数,可以考虑平方根的形式。因为$3^2 = 9$,$4^2 = 16$,所以只要找到一个被开方数在9和16之间且不是完全平方数的数,其算术平方根就是3和4之间的无理数。例如$\sqrt{10}$,因为$9 < 10 < 16$,所以$3 < \sqrt{10} < 4$,且$\sqrt{10}$是无理数。
【答案】:$\sqrt{10}$(答案不唯一)
【答案】:$\sqrt{10}$(答案不唯一)
5. (★★★)$1-\sqrt {5}$的相反数是______,绝对值是______.
答案:
【解析】:根据相反数的定义,只有符号不同的两个数互为相反数,所以$1 - \sqrt{5}$的相反数是$-(1 - \sqrt{5}) = \sqrt{5} - 1$。
因为$\sqrt{5} \approx 2.236$,所以$1 - \sqrt{5} \approx 1 - 2.236 = -1.236$,是负数。根据绝对值的性质,负数的绝对值是它的相反数,所以$|1 - \sqrt{5}| = \sqrt{5} - 1$。
【答案】:$\sqrt{5}-1$,$\sqrt{5}-1$
因为$\sqrt{5} \approx 2.236$,所以$1 - \sqrt{5} \approx 1 - 2.236 = -1.236$,是负数。根据绝对值的性质,负数的绝对值是它的相反数,所以$|1 - \sqrt{5}| = \sqrt{5} - 1$。
【答案】:$\sqrt{5}-1$,$\sqrt{5}-1$
6. (★★★)如果$\sqrt {10}$在两个连续整数a和b之间,即$a<\sqrt {10}<b$,那么a,b的值分别是______.
答案:
【解析】:因为$3^2 = 9$,$4^2 = 16$,而$9 < 10 < 16$,所以$\sqrt{9} < \sqrt{10} < \sqrt{16}$,即$3 < \sqrt{10} < 4$。因此,$a = 3$,$b = 4$。
【答案】:3,4
【答案】:3,4
7. (★★)在数轴上离原点距离是$\sqrt {5}$的点表示的数是______.
答案:
【解析】:在数轴上,一个点到原点的距离等于这个点所表示的数的绝对值。设该点表示的数为$x$,则$|x| = \sqrt{5}$,所以$x = \pm\sqrt{5}$。
【答案】:$\pm\sqrt{5}$
【答案】:$\pm\sqrt{5}$
8. (★★)若$x^{2}= 12$,则x是一个______数,x的整数部分是______.
答案:
【解析】:因为$x^{2}=12$,所以$x = \pm\sqrt{12} = \pm2\sqrt{3}$。由于$\sqrt{3}$是无理数,所以$2\sqrt{3}$也是无理数,即$x$是一个无理数。
又因为$9 < 12 < 16$,所以$\sqrt{9} < \sqrt{12} < \sqrt{16}$,即$3 < \sqrt{12} < 4$,所以$\sqrt{12}$的整数部分是$3$,那么$-\sqrt{12}$的整数部分是$-4$,但题目问的是$x$的整数部分,这里通常指的是算术平方根对应的整数部分,所以$x$的整数部分是$3$。
【答案】:无理;3
又因为$9 < 12 < 16$,所以$\sqrt{9} < \sqrt{12} < \sqrt{16}$,即$3 < \sqrt{12} < 4$,所以$\sqrt{12}$的整数部分是$3$,那么$-\sqrt{12}$的整数部分是$-4$,但题目问的是$x$的整数部分,这里通常指的是算术平方根对应的整数部分,所以$x$的整数部分是$3$。
【答案】:无理;3
9. (★★★)直径为1个单位长度的圆,从数轴上的原点向右滚动一周,圆上的一点由原点滚动到$O'$,则点$O'$所表示的数是______.
答案:
【解析】:直径为1个单位长度的圆,其周长为$C = \pi d = \pi×1 = \pi$。当圆从原点向右滚动一周时,圆上的点$O$滚动到$O'$,点$O'$所经过的路程就是圆的周长,所以点$O'$在数轴上所表示的数是$\pi$。
【答案】:$\pi$
【答案】:$\pi$
10. (★★★)大于$-\sqrt {17}而小于\sqrt {11}$的所有整数的和是______.
答案:
【解析】:首先,估算$-\sqrt{17}$和$\sqrt{11}$的取值范围。因为$\sqrt{16} = 4$,$\sqrt{25} = 5$,所以$4 < \sqrt{17} < 5$,进而可得$-5 < -\sqrt{17} < -4$。又因为$\sqrt{9} = 3$,$\sqrt{16} = 4$,所以$3 < \sqrt{11} < 4$。
接下来,找出大于$-\sqrt{17}$而小于$\sqrt{11}$的所有整数。大于$-5$且小于$4$的整数有$-4$,$-3$,$-2$,$-1$,$0$,$1$,$2$,$3$。
然后,计算这些整数的和:$(-4) + (-3) + (-2) + (-1) + 0 + 1 + 2 + 3$。通过分组计算,$(-4) + 0 = -4$,$(-3 + 3) = 0$,$(-2 + 2) = 0$,$(-1 + 1) = 0$,所以总和为$-4$。
【答案】:-4
接下来,找出大于$-\sqrt{17}$而小于$\sqrt{11}$的所有整数。大于$-5$且小于$4$的整数有$-4$,$-3$,$-2$,$-1$,$0$,$1$,$2$,$3$。
然后,计算这些整数的和:$(-4) + (-3) + (-2) + (-1) + 0 + 1 + 2 + 3$。通过分组计算,$(-4) + 0 = -4$,$(-3 + 3) = 0$,$(-2 + 2) = 0$,$(-1 + 1) = 0$,所以总和为$-4$。
【答案】:-4
11. (★★★)比较无理数的大小:(1)$5\sqrt {6}和6\sqrt {5}$;(2)$-\frac {\sqrt {7}}{2}和-\frac {π}{3}$.
答案:
(1)
∵ $5\sqrt{6} = \sqrt{5^2 × 6} = \sqrt{150}$,$6\sqrt{5} = \sqrt{6^2 × 5} = \sqrt{180}$
∵ $\sqrt{150} < \sqrt{180}$
∴ $5\sqrt{6} < 6\sqrt{5}$
(2)
∵ $\sqrt{7} \approx 2.6458$,$\frac{\sqrt{7}}{2} \approx 1.3229$
∵ $π \approx 3.1416$,$\frac{π}{3} \approx 1.0472$
∵ $1.3229 > 1.0472$
∴ $-\frac{\sqrt{7}}{2} < -\frac{π}{3}$
(1)
∵ $5\sqrt{6} = \sqrt{5^2 × 6} = \sqrt{150}$,$6\sqrt{5} = \sqrt{6^2 × 5} = \sqrt{180}$
∵ $\sqrt{150} < \sqrt{180}$
∴ $5\sqrt{6} < 6\sqrt{5}$
(2)
∵ $\sqrt{7} \approx 2.6458$,$\frac{\sqrt{7}}{2} \approx 1.3229$
∵ $π \approx 3.1416$,$\frac{π}{3} \approx 1.0472$
∵ $1.3229 > 1.0472$
∴ $-\frac{\sqrt{7}}{2} < -\frac{π}{3}$
12. (★★★)计算.
(1)$3(\sqrt {2}+\sqrt {3})+3(\sqrt {2}-2\sqrt {3})$;
(2)$|2-\sqrt {5}|-|\sqrt {5}-1|$.
(1)$3(\sqrt {2}+\sqrt {3})+3(\sqrt {2}-2\sqrt {3})$;
(2)$|2-\sqrt {5}|-|\sqrt {5}-1|$.
答案:
【解析】:
(1) 原式$=3\sqrt{2}+3\sqrt{3}+3\sqrt{2}-6\sqrt{3}=(3\sqrt{2}+3\sqrt{2})+(3\sqrt{3}-6\sqrt{3})=6\sqrt{2}-3\sqrt{3}$;
(2) 因为$\sqrt{5}\approx2.236$,所以$2-\sqrt{5}\lt0$,$\sqrt{5}-1\gt0$,则原式$=(\sqrt{5}-2)-(\sqrt{5}-1)=\sqrt{5}-2-\sqrt{5}+1=-1$。
【答案】:
(1)$6\sqrt{2}-3\sqrt{3}$;
(2)$-1$
(1) 原式$=3\sqrt{2}+3\sqrt{3}+3\sqrt{2}-6\sqrt{3}=(3\sqrt{2}+3\sqrt{2})+(3\sqrt{3}-6\sqrt{3})=6\sqrt{2}-3\sqrt{3}$;
(2) 因为$\sqrt{5}\approx2.236$,所以$2-\sqrt{5}\lt0$,$\sqrt{5}-1\gt0$,则原式$=(\sqrt{5}-2)-(\sqrt{5}-1)=\sqrt{5}-2-\sqrt{5}+1=-1$。
【答案】:
(1)$6\sqrt{2}-3\sqrt{3}$;
(2)$-1$
查看更多完整答案,请扫码查看


