《2025年Happy暑假作业快乐暑假武汉大学出版社七年级数学》

1. (★★)如图,$∠1与∠2$是对顶角的是 ( )

答案： 【解析】：对顶角的定义为：如果一个角的两边分别是另一个角两边的反向延长线，且这两个角有公共顶点，那么这两个角是对顶角。
选项A：∠1与∠2的两边不互为反向延长线，不是对顶角。
选项B：∠1与∠2的两边不互为反向延长线，不是对顶角。
选项C：∠1与∠2有一条边在同一直线上，但另一条边不是反向延长线，不是对顶角。
选项D：∠1与∠2有公共顶点，且两边分别互为反向延长线，符合对顶角的定义。
【答案】：D

2. (★★)下列选项图中,$∠1和∠2$是同位角的是 ( )

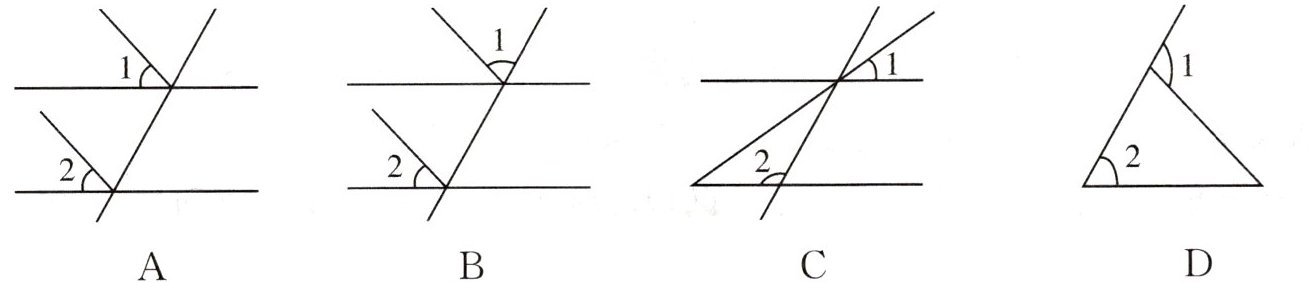
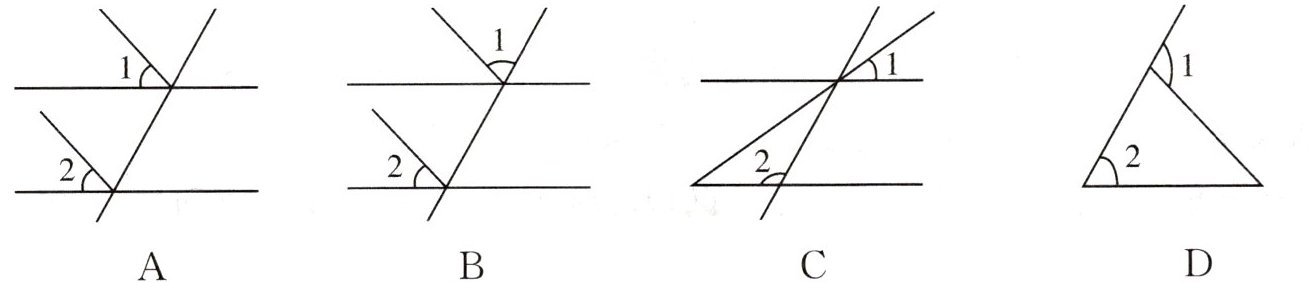
答案： 【解析】：同位角的定义为：两条直线被第三条直线所截，在截线的同旁，被截两直线的同一侧的角，我们把这样的两个角称为同位角。其位置特征可概括为“F”型。
选项A：∠1和∠2由三条直线形成，其中∠1是由上面的水平直线、倾斜直线被另一条倾斜直线所截形成，∠2是由下面的水平直线、倾斜直线被另一条倾斜直线所截形成，它们不是由两条直线被第三条直线所截得到的，不满足同位角的前提条件，所以不是同位角。
选项B：∠1和∠2是两条水平直线被一条倾斜直线所截形成的角，它们都在截线（倾斜直线）的右侧，且分别在两条被截直线（两条水平直线）的上方，符合“F”型特征，满足同位角的定义，是同位角。
选项C：∠1和∠2的边所在直线不同，∠1的两边是一条水平直线和一条倾斜直线，∠2的两边是另一条倾斜直线和水平直线，它们的位置关系不符合同位角在截线同旁、被截直线同一侧的特征，不是同位角。
选项D：∠1和∠2是三角形的两个内角，是由三角形的三条边所形成的角，并非两条直线被第三条直线所截得到的角，不符合同位角的定义，不是同位角。
【答案】：B

3. (★★★)如图所示,$∠AOB= ∠COD= 90^{\circ }$,则下列叙述中正确的是 ( )


A.$∠AOC= ∠AOD$
B.$∠AOD= ∠BOD$
C.$∠AOC= ∠BOD$
D.以上都不对

答案： 【解析】：已知$\angle AOB = \angle COD = 90^{\circ}$，观察图形可知$\angle AOB$由$\angle AOD$和$\angle DOB$组成，即$\angle AOD+\angle DOB = 90^{\circ}$；$\angle COD$由$\angle COA$和$\angle AOD$组成，即$\angle COA+\angle AOD = 90^{\circ}$。因为$\angle AOD+\angle DOB=\angle COA+\angle AOD$，等式两边同时减去$\angle AOD$，可得$\angle AOC=\angle BOD$。
【答案】：C

4. (★★★)如图,在三角形 ABC 中,$AC⊥BC,CD⊥AB$,则下列关系不成立的是( )


A.$AB＞AC＞AD$
B.$AB＞BC＞CD$
C.$AC+BC＞AB$
D.$AC＞CD＞BC$

答案： 【解析】：在直角三角形ABC中，AC⊥BC，所以AB是斜边，根据直角三角形斜边最长，可得AB＞AC且AB＞BC。
在直角三角形ACD中，AC是斜边，CD是直角边，所以AC＞CD；同理在直角三角形BCD中，BC＞CD。
在直角三角形ACD中，AD是直角边，AC是斜边，所以AC＞AD；同理在直角三角形BCD中，BC＞BD。
对于选项A：AB＞AC（斜边大于直角边），AC＞AD（直角三角形中斜边大于直角边），所以AB＞AC＞AD成立。
对于选项B：AB＞BC（斜边大于直角边），BC＞CD（直角三角形中斜边大于直角边），所以AB＞BC＞CD成立。
对于选项C：根据三角形三边关系，任意两边之和大于第三边，所以AC+BC＞AB成立。
对于选项D：AC和BC都是直角三角形ABC的直角边，无法确定AC和BC的大小关系，所以AC＞CD＞BC不一定成立，比如当AC=3，BC=4时，CD=（AC×BC）/AB=12/5=2.4，此时BC=4＞CD=2.4，AC=3＞CD=2.4，但AC=3＜BC=4，所以AC＞CD＞BC不成立。
【答案】：D

5. (★★★)在两条直线相交所成的四个角中,下列条件不能判定这两条直线垂直的是 ( )

A.对顶角互补
B.四对邻补角
C.三个角相等
D.邻补角相等

答案： 【解析】：两条直线相交所成的四个角中，若两条直线垂直，则四个角均为直角（90°）。
选项A：对顶角相等且互补，即对顶角之和为180°，则每个角为90°，可判定垂直。
选项B：任意两条直线相交，都会形成四对邻补角（每个角与相邻的角互补），这是相交线的基本性质，与是否垂直无关，不能判定垂直。
选项C：四个角之和为360°，若三个角相等，则每个角为360°÷4=90°（第四个角也与它们相等），可判定垂直。
选项D：邻补角互补且相等，即每个角为90°，可判定垂直。
【答案】：B

6. (★★★)如图,$OA⊥OB$于点 O,直线 CD 经过点 O,$∠AOD= 35^{\circ }$,则$∠BOC= $____.

答案： 解：
∵OA⊥OB
∴∠AOB=90°（垂直的定义）
∵∠AOD=35°
∴∠DOB=∠AOB - ∠AOD=90° - 35°=55°
∵直线CD经过点O
∴∠COD=180°（平角的定义）
∴∠BOC=∠COD - ∠DOB=180° - 55°=125°
125°

7. (★★★)如图,$OD⊥BC$,垂足为 D,$BD= 6cm,OD= 8cm,OB= 10cm$,那么点 B 到 OD 的距离为____,点 O 到 BC 的距离为____,O,B 两点间的距离为____.

答案： 【解析】：点到直线的距离是指从这点向直线所作垂线段的长度。因为 $OD⊥BC$，所以点 $B$ 到 $OD$ 的距离是线段 $BD$ 的长度，已知 $BD = 6cm$；点 $O$ 到 $BC$ 的距离是线段 $OD$ 的长度，已知 $OD = 8cm$；$O$、$B$ 两点间的距离是线段 $OB$ 的长度，已知 $OB = 10cm$。
【答案】：6cm,8cm,10cm