《2025年Happy暑假作业快乐暑假武汉大学出版社七年级数学》

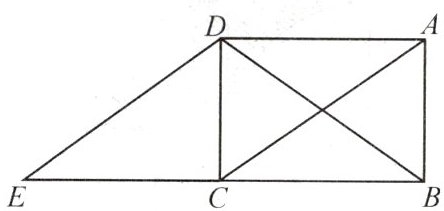
13. (★★★)如图,在长方形 $ABCD$ 中,$AB = 4$,$BC = 5$,连接对角线 $AC$,$BD$. 如果 $AC // DE$,$AD // EC$,那么三角形 $DCE$ 可以看成是由哪个三角形平移得到的?请指出平移的方向和距离,并求出四边形 $ACED$ 的面积.

答案： 【解析】：在长方形 $ABCD$ 中，$AD// BC$，$AD = BC = 5$，$AB = CD = 4$。
因为 $AC// DE$，$AD// EC$，所以四边形 $ACED$ 是平行四边形，因此 $AD = EC = 5$，$AC = DE$。
在平行四边形中，对边平行且相等，所以点 $A$ 平移到点 $D$，点 $C$ 平移到点 $E$，即 $\triangle DCE$ 可由 $\triangle ACD$ 平移得到。平移方向为从点 $A$ 到点 $D$ 的方向（或向下），距离为 $AD$ 的长度，即 $5$。
四边形 $ACED$ 的面积：由于 $AD// EC$ 且 $AD = EC$，四边形 $ACED$ 是平行四边形，其底为 $AD = 5$，高为 $CD = 4$（因为 $CD$ 垂直于 $AD$ 和 $EC$），所以面积为 $底×高=5×4 = 20$。
【答案】：三角形 $ACD$；平移方向是从点 $A$ 到点 $D$ 的方向（或向下）；平移距离是 $5$；四边形 $ACED$ 的面积是 $20$。

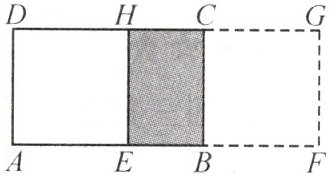
14. (★★★★)如图,在长方形 $ABCD$ 中,$AB = 10 \mathrm{~cm}$,$BC = 6 \mathrm{~cm}$,试问:将长方形 $ABCD$ 沿着 $AB$ 方向平移多少才能使平移后的长方形与原来的长方形 $ABCD$ 重叠部分的面积为 $24 \mathrm{~cm}^2$?

答案： 【解析】：设长方形沿着 $AB$ 方向平移的距离为 $x\ \text{cm}$。
原长方形 $ABCD$ 中，$AB = 10\ \text{cm}$，$BC = 6\ \text{cm}$。平移后，重叠部分是一个长方形，其宽仍为 $BC = 6\ \text{cm}$，长为 $AB - x = (10 - x)\ \text{cm}$（当向右平移时，重叠部分的长为原长减去平移距离）。
根据重叠部分面积为 $24\ \text{cm}^2$，可得方程：
$6(10 - x) = 24$
解得：
$10 - x = 4 \implies x = 6$
【答案】：6

如图,点 $A$,$B$ 为湖畔的两座村庄,为了测量两村庄之间的距离.请你设计一个测量方案,并说明你的理由.

答案： 【解析】：在湖岸选择一个可以直接到达A、B两点的点C，连接AC并延长到点D，使CD=AC；连接BC并延长到点E，使CE=BC。然后测量DE的长度，DE的长度即为A、B两村庄之间的距离。理由：在△ABC和△DEC中，AC=DC，∠ACB=∠DCE（对顶角相等），BC=EC，根据“SAS”（边角边）全等判定定理可得△ABC≌△DEC，所以AB=DE（全等三角形对应边相等）。
【答案】：在湖岸选一点C，使C可直达A、B，延长AC到D使CD=AC，延长BC到E使CE=BC，测量DE长即为AB长。