2025年核心素养天天练六年级数学下册冀教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年核心素养天天练六年级数学下册冀教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第36页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
四 按要求做题。(每题8分,共16分)
1.计算下面图形的体积。(单位:分米)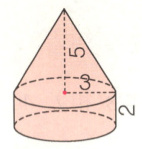
2.求阴影部分的体积。(单位:厘米)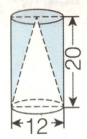
1.计算下面图形的体积。(单位:分米)

2.求阴影部分的体积。(单位:厘米)

答案:
答案:1.3.14×3²×2+3.14×3²×5×$\frac{1}{3}$=103.62(立方分米)
2.3.14×(12÷2)²×20×(1−$\frac{1}{3}$)=1507.2(立方厘米)
解析:1. 该图形是由一个圆柱和一个圆锥组成,圆柱体积公式$V_1 = \pi r²h_1$,圆锥体积公式$V_2 = \frac{1}{3}\pi r²h_2$,这里$r = 3$分米,$h_1 = 2$分米,$h_2 = 5$分米,总体积$V = V_1 + V_2 = 3.14×3²×2 + 3.14×3²×5×\frac{1}{3} = 103.62$立方分米。
2. 阴影部分体积等于大圆柱体积减去圆锥体积,大圆柱体积$V_1 = \pi r²h$,圆锥体积$V_2 = \frac{1}{3}\pi r²h$,这里$r = 12÷2 = 6$厘米,$h = 20$厘米,阴影部分体积$V = V_1 - V_2 = 3.14×(12÷2)²×20×(1 - \frac{1}{3}) = 1507.2$立方厘米。
2.3.14×(12÷2)²×20×(1−$\frac{1}{3}$)=1507.2(立方厘米)
解析:1. 该图形是由一个圆柱和一个圆锥组成,圆柱体积公式$V_1 = \pi r²h_1$,圆锥体积公式$V_2 = \frac{1}{3}\pi r²h_2$,这里$r = 3$分米,$h_1 = 2$分米,$h_2 = 5$分米,总体积$V = V_1 + V_2 = 3.14×3²×2 + 3.14×3²×5×\frac{1}{3} = 103.62$立方分米。
2. 阴影部分体积等于大圆柱体积减去圆锥体积,大圆柱体积$V_1 = \pi r²h$,圆锥体积$V_2 = \frac{1}{3}\pi r²h$,这里$r = 12÷2 = 6$厘米,$h = 20$厘米,阴影部分体积$V = V_1 - V_2 = 3.14×(12÷2)²×20×(1 - \frac{1}{3}) = 1507.2$立方厘米。
1.[唐山市路北区期末]一个圆柱形的玻璃鱼缸(无盖),底面直径是2分米,高是3分米。如果玻璃厚度忽略不计。
(1)做一个这样的鱼缸至少需要多少平方分米的玻璃? (8分)
(2)在鱼缸中倒入一些水,水深2分米,鱼缸中有多少升水? (8分)
(1)做一个这样的鱼缸至少需要多少平方分米的玻璃? (8分)
(2)在鱼缸中倒入一些水,水深2分米,鱼缸中有多少升水? (8分)
答案:
答案:
(1)3.14×(2÷2)²+3.14×2×3=21.98(平方分米)
(2)3.14×(2÷2)²×2=6.28(立方分米)
6.28立方分米=6.28升
解析:
(1) 无盖鱼缸的表面积等于一个底面积加上侧面积,底面积$S_1 = \pi r²$,侧面积$S_2 = \pi dh$,这里$d = 2$分米,$h = 3$分米,$r = 2÷2 = 1$分米,所以表面积$S = S_1 + S_2 = 3.14×(2÷2)² + 3.14×2×3 = 21.98$平方分米。
(2) 水的体积等于底面积乘以水深,底面积$S = \pi r²$,$r = 2÷2 = 1$分米,水深$h = 2$分米,所以水的体积$V = 3.14×(2÷2)²×2 = 6.28$立方分米,因为$1$立方分米$ = 1$升,所以$6.28$立方分米$ = 6.28$升。
(1)3.14×(2÷2)²+3.14×2×3=21.98(平方分米)
(2)3.14×(2÷2)²×2=6.28(立方分米)
6.28立方分米=6.28升
解析:
(1) 无盖鱼缸的表面积等于一个底面积加上侧面积,底面积$S_1 = \pi r²$,侧面积$S_2 = \pi dh$,这里$d = 2$分米,$h = 3$分米,$r = 2÷2 = 1$分米,所以表面积$S = S_1 + S_2 = 3.14×(2÷2)² + 3.14×2×3 = 21.98$平方分米。
(2) 水的体积等于底面积乘以水深,底面积$S = \pi r²$,$r = 2÷2 = 1$分米,水深$h = 2$分米,所以水的体积$V = 3.14×(2÷2)²×2 = 6.28$立方分米,因为$1$立方分米$ = 1$升,所以$6.28$立方分米$ = 6.28$升。
2.在一个底面直径是20厘米的圆柱形水槽中,放入一个底面直径是10厘米的圆锥形零件,水面上升了2厘米,这个圆锥形零件的高是多少厘米? (圆锥形零件完全浸没且水未溢出)(8分)
答案:
答案:3.14×($\frac{20}{2}$)²×2×3÷[3.14×($\frac{10}{2}$)²]=24(厘米)
解析:圆锥形零件的体积等于上升的水的体积,上升的水是一个底面直径为20厘米,高为2厘米的圆柱,根据圆柱体积公式$V_1 = \pi r_1²h$($r_1 = 20÷2 = 10$厘米,$h = 2$厘米),可得上升的水的体积$V_1 = 3.14×(\frac{20}{2})²×2$。圆锥体积公式$V_2 = \frac{1}{3}\pi r_2²H$($r_2 = 10÷2 = 5$厘米),因为$V_1 = V_2$,所以$H = 3.14×(\frac{20}{2})²×2×3÷[3.14×(\frac{10}{2})²] = 24$厘米。
解析:圆锥形零件的体积等于上升的水的体积,上升的水是一个底面直径为20厘米,高为2厘米的圆柱,根据圆柱体积公式$V_1 = \pi r_1²h$($r_1 = 20÷2 = 10$厘米,$h = 2$厘米),可得上升的水的体积$V_1 = 3.14×(\frac{20}{2})²×2$。圆锥体积公式$V_2 = \frac{1}{3}\pi r_2²H$($r_2 = 10÷2 = 5$厘米),因为$V_1 = V_2$,所以$H = 3.14×(\frac{20}{2})²×2×3÷[3.14×(\frac{10}{2})²] = 24$厘米。
3.一块长方形的塑料板,利用图中阴影部分刚好能做成一个圆柱形的带盖水桶(接头处忽略不计)。这个水桶的表面积是多少? (9分)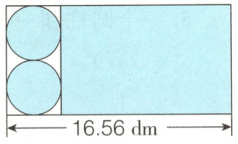

答案:
答案:16.56÷(1+3.14)=4(分米)
4×2=8(分米)
3.14×($\frac{4}{2}$)²×2+3.14×4×8=125.6(平方分米)
解析:设圆的直径为$d$,由图可知长方形的长等于底面圆的周长加上直径,即$d + \pi d = 16.56$,$d(1 + 3.14) = 16.56$,解得$d = 4$分米,那么圆柱的高$h = 2d = 8$分米。水桶表面积等于两个底面积加上侧面积,底面积$S_1 = \pi r²$($r = 4÷2 = 2$分米),侧面积$S_2 = \pi dh$,所以表面积$S = 2S_1 + S_2 = 3.14×(\frac{4}{2})²×2 + 3.14×4×8 = 125.6$平方分米。
4×2=8(分米)
3.14×($\frac{4}{2}$)²×2+3.14×4×8=125.6(平方分米)
解析:设圆的直径为$d$,由图可知长方形的长等于底面圆的周长加上直径,即$d + \pi d = 16.56$,$d(1 + 3.14) = 16.56$,解得$d = 4$分米,那么圆柱的高$h = 2d = 8$分米。水桶表面积等于两个底面积加上侧面积,底面积$S_1 = \pi r²$($r = 4÷2 = 2$分米),侧面积$S_2 = \pi dh$,所以表面积$S = 2S_1 + S_2 = 3.14×(\frac{4}{2})²×2 + 3.14×4×8 = 125.6$平方分米。
4.[石家庄市新华区期末]如图,一种饮料瓶瓶身呈圆柱形(瓶颈部分忽略不计),它的底面直径是8厘米,正着摆放时瓶中饮料的高度是10厘米,倒着摆放时瓶中空余部分的高度是4厘米,饮料瓶的容积是多少? (10分)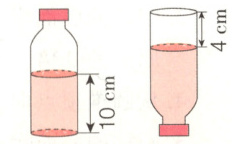

答案:
答案:3.14×(8÷2)²×(10+4)=703.36(立方厘米)
解析:饮料瓶的容积等于饮料的体积加上倒着放时空余部分的体积,而这两部分合起来相当于一个底面直径为8厘米,高为$(10 + 4)$厘米的圆柱的体积。根据圆柱体积公式$V = \pi r²h$($r = 8÷2 = 4$厘米,$h = 10 + 4 = 14$厘米),可得容积$V = 3.14×(8÷2)²×(10 + 4) = 703.36$立方厘米。
解析:饮料瓶的容积等于饮料的体积加上倒着放时空余部分的体积,而这两部分合起来相当于一个底面直径为8厘米,高为$(10 + 4)$厘米的圆柱的体积。根据圆柱体积公式$V = \pi r²h$($r = 8÷2 = 4$厘米,$h = 10 + 4 = 14$厘米),可得容积$V = 3.14×(8÷2)²×(10 + 4) = 703.36$立方厘米。
查看更多完整答案,请扫码查看


