1. 在Rt△ABC中,两条直角边长分别为1,2,则斜边长为 ( )
A.1
B.2
C.$\sqrt{3}$
D.$\sqrt{5}$
A.1
B.2
C.$\sqrt{3}$
D.$\sqrt{5}$
答案:
D
2. 下列四组数:①3,4,5;②$\frac{1}{3}$,$\frac{1}{4}$,$\frac{1}{5}$;③0.3,0.4,0.5;④8,15,17.其中是勾股数的有 ( )
A.4组
B.3组
C.2组
D.1组
A.4组
B.3组
C.2组
D.1组
答案:
C
3. 如图,已知一轮船以16海里/时的速度从港口A出发向东北方向航行,另一轮船以12海里/时的速度同时从港口A出发向东南方向航行,离开港口2小时后,两船相距 ( )
A.25海里 B.30海里
C.35海里 D.40海里

A.25海里 B.30海里
C.35海里 D.40海里

答案:
D
4. 如图,已知圆柱底面的周长为8dm,高为3dm,在圆柱的侧面上,过点A和点C嵌有一圈金属丝,则这圈金属丝的周长最小为 ( )
A.11dm B.2$\sqrt{55}$dm
C.2$\sqrt{73}$dm D.10dm

A.11dm B.2$\sqrt{55}$dm
C.2$\sqrt{73}$dm D.10dm

答案:
D
5. 在△ABC中,∠C=90°,且BC=9,AB=41,则AC的长为______.
答案:
40
6. 有一根旗杆在离地面9米处断裂,旗杆顶部落在离旗杆底部12米处,旗杆折断之前有______米高.
答案:
24
7. 如图,A,B为数轴上两点,AB=3,过点B作BC⊥AB,且BC=2.以点A为圆心、AC的长为半径作圆交数轴于点P.若点P所表示的数是$\sqrt{13}-2$,则点A表示的数是______.
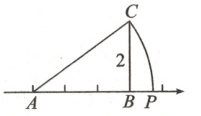

答案:
- 2
8. (9分)如图,点E在正方形ABCD内,满足∠AEB=90°,AE=8,BE=6,求图中阴影部分的面积.
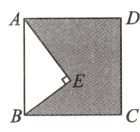

答案:
解:在Rt△ABE中,∠AEB = 90°,由勾股定理,得AB² = AE² + BE² = 8² + 6² = 100,
∴AB = 10,
∴正方形ABCD的面积是10×10 = 100.又
∵△ABE的面积是$\frac{1}{2}$AE·BE = $\frac{1}{2}$×8×6 = 24,
∴阴影部分的面积是100 - 24 = 76.
∴AB = 10,
∴正方形ABCD的面积是10×10 = 100.又
∵△ABE的面积是$\frac{1}{2}$AE·BE = $\frac{1}{2}$×8×6 = 24,
∴阴影部分的面积是100 - 24 = 76.
9. (10分)某路段限速标志规定:小汽车在此路段上的行驶速度不得超过70km/h.如图,一辆小汽车在该笔直路段l上行驶,某一时刻刚好行驶到路对面的车速检测仪A的正前方30m的点C处,2s后小汽车行驶到点B处,测得此时小汽车与车速检测仪A间的距离为50m.
(1)求BC的长;
(2)这辆小汽车超速了吗? 并说明理由.
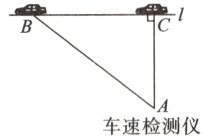
(1)求BC的长;
(2)这辆小汽车超速了吗? 并说明理由.

答案:
(1)解:根据题意,得∠ACB = 90°,AC = 30m,AB = 50m,
∴BC = $\sqrt{AB^{2}-AC^{2}}$ = $\sqrt{50^{2}-30^{2}}$ = 40(m).答:BC的长为40m.
(2)这辆小汽车超速了.理由如下:
∵该小汽车的速度为40÷2 = 20(m/s) = 72(km/h)>70km/h,
∴这辆小汽车超速了.
(1)解:根据题意,得∠ACB = 90°,AC = 30m,AB = 50m,
∴BC = $\sqrt{AB^{2}-AC^{2}}$ = $\sqrt{50^{2}-30^{2}}$ = 40(m).答:BC的长为40m.
(2)这辆小汽车超速了.理由如下:
∵该小汽车的速度为40÷2 = 20(m/s) = 72(km/h)>70km/h,
∴这辆小汽车超速了.
查看更多完整答案,请扫码查看


