1.已知一次函数的图象经过点(0,−2)和点(1,−1),则这个函数的解析式为 ( )
A. $y = x - 2$
B. $y = x + 2$
C. $y = -x - 2$
D. $y = -x + 2$
A. $y = x - 2$
B. $y = x + 2$
C. $y = -x - 2$
D. $y = -x + 2$
答案:
A
2.(呼和浩特市中考)在平面直角坐标系中,点$A(3,0)$,$B(0,4)$。以$AB$为一边在第一象限作正方形$ABCD$,则对角线$BD$所在直线的解析式为 ( )
A. $y = -\frac{1}{7}x + 4$
B. $y = -\frac{1}{4}x + 4$
C. $y = -\frac{1}{2}x + 4$
D. $y = 4$
A. $y = -\frac{1}{7}x + 4$
B. $y = -\frac{1}{4}x + 4$
C. $y = -\frac{1}{2}x + 4$
D. $y = 4$
答案:
A
3.将直线$y = 2x$向右平移1个单位后所得图象对应的函数解析式为 ( )
A. $y = 2x - 1$
B. $y = 2x - 2$
C. $y = 2x + 1$
D. $y = 2x + 2$
A. $y = 2x - 1$
B. $y = 2x - 2$
C. $y = 2x + 1$
D. $y = 2x + 2$
答案:
B
4.如图,直线$AB$的解析式是______________.
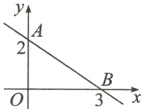

答案:
$y = -\frac{2}{3}x + 2$
5.已知$y$是$x$的一次函数,如表列出了部分对应值,则$m =$_______.


答案:
-0.5
6.与直线$y = 5x + 1$关于$y$轴对称的直线解析式是________________.
答案:
$y = -5x + 1$
7.把直线$y = -3x$向上平移后得到直线$AB$,直线$AB$经过点$(2,-3)$,则直线$AB$的函数解析式是________________.
答案:
$y = -3x + 3$
8.如图,直线$AB$与$x$轴交于点$A(1,0)$,与$y$轴交于点$B(0,-2)$。
(1)求直线$AB$的函数解析式;
(2)若直线$AB$上存在一点$D$,且$S_{\triangle BOD}=2$,求点$D$的坐标。
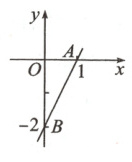
(1)求直线$AB$的函数解析式;
(2)若直线$AB$上存在一点$D$,且$S_{\triangle BOD}=2$,求点$D$的坐标。

答案:
(1)解:设直线AB的函数解析式为$y = kx + b(k\neq0)$.
∵直线AB过点$A(1,0)$,$B(0,-2)$,$\therefore\begin{cases}k + b = 0\\b = -2\end{cases}$, 解得$\begin{cases}k = 2\\b = -2\end{cases}$.
∴直线AB的函数解析式为$y = 2x - 2$.
(2)设点D的坐标为$(x,y)$. $\because S_{\triangle BOD}=2$,$\therefore\frac{1}{2}\times2\times|x| = 2$. 解得$x = \pm2$. 当$x = 2$时,$y = 2\times2 - 2 = 2$; 当$x = -2$时,$y = 2\times(-2) - 2 = -6$. $\therefore$点D的坐标为$(2,2)$或$(-2,-6)$.
(1)解:设直线AB的函数解析式为$y = kx + b(k\neq0)$.
∵直线AB过点$A(1,0)$,$B(0,-2)$,$\therefore\begin{cases}k + b = 0\\b = -2\end{cases}$, 解得$\begin{cases}k = 2\\b = -2\end{cases}$.
∴直线AB的函数解析式为$y = 2x - 2$.
(2)设点D的坐标为$(x,y)$. $\because S_{\triangle BOD}=2$,$\therefore\frac{1}{2}\times2\times|x| = 2$. 解得$x = \pm2$. 当$x = 2$时,$y = 2\times2 - 2 = 2$; 当$x = -2$时,$y = 2\times(-2) - 2 = -6$. $\therefore$点D的坐标为$(2,2)$或$(-2,-6)$.
9.如图,一次函数$y = -\frac{2}{3}x + 2$的图象分别与$x$轴、$y$轴交于点$A$,$B$,以线段$AB$为边在第一象限内作等腰直角$\triangle ABC$,$\angle BAC = 90^{\circ}$,求过$B$,$C$两点的直线的解析式。
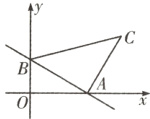

答案:
解:一次函数$y = -\frac{2}{3}x + 2$中,令$x = 0$,得$y = 2$; 令$y = 0$,得$x = 3$. $\therefore A$的坐标是$(3,0)$,$B$的坐标是$(0,2)$. 作$CD\perp x$轴于点D. $\because\angle BAC = 90^{\circ}$,$\therefore\angle OAB+\angle CAD = 90^{\circ}$. 又$\because\angle CAD+\angle ACD = 90^{\circ}$,$\therefore\angle ACD = \angle OAB$. $\because AB = AC$,$\angle BOA=\angle CDA = 90^{\circ}$,$\therefore\triangle ABO\cong\triangle CAD(AAS)$,$\therefore AD = OB = 2$,$CD = OA = 3$,$OD = OA + AD = 5$. $\therefore C$的坐标是$(5,3)$. 设直线BC的解析式是$y = kx + b$,根据题意得$\begin{cases}b = 2\\5k + b = 3\end{cases}$, 解得$\begin{cases}k = \frac{1}{5}\\b = 2\end{cases}$. $\therefore$直线BC的解析式是$y = \frac{1}{5}x + 2$.
查看更多完整答案,请扫码查看


