1.下面是嘉嘉作业本上的一道习题及解答过程:
已知:如图所示,△ABC中,AB=AC,AE 平分△ABC的外角∠CAN,点M是AC 的中点,连接BM并延长交AE于点D,连接CD.

求证:四边形ABCD
是平行四边形.
证明:∵AB=AC,
∴∠ABC=∠3.
∵∠CAN=∠ABC+∠3,∠CAN=∠1+∠2,∠1=∠2,
∴ ① .
又∵∠4=∠5,MA=MC,
∴△MAD≌△MCB( ② ).
∴MD=MB.
∴四边形ABCD是平行四边形.
若以上解答过程正确,①,②应分别为( )
A.∠1=∠3,AAS
B.∠1=∠3,ASA
C.∠2=∠3,AAS
D.∠2=∠3,ASA
已知:如图所示,△ABC中,AB=AC,AE 平分△ABC的外角∠CAN,点M是AC 的中点,连接BM并延长交AE于点D,连接CD.

求证:四边形ABCD
是平行四边形.
证明:∵AB=AC,
∴∠ABC=∠3.
∵∠CAN=∠ABC+∠3,∠CAN=∠1+∠2,∠1=∠2,
∴ ① .
又∵∠4=∠5,MA=MC,
∴△MAD≌△MCB( ② ).
∴MD=MB.
∴四边形ABCD是平行四边形.
若以上解答过程正确,①,②应分别为( )
A.∠1=∠3,AAS
B.∠1=∠3,ASA
C.∠2=∠3,AAS
D.∠2=∠3,ASA
答案:
D
2.(原创题)如图,已知∠MAN.请按下面步骤作图:在AM上取一点B,在AN上取一点C,分别以点B,C为圆心,AC,AB的长为半径画弧,两弧在∠MAN内交于一点D,连接BD,CD.则四边形ABDC是______________形,理由是________________.
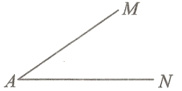

答案:
平行四边 两组对边分别相等的四边形是平行四边形 解:所画图形如图所示.
平行四边 两组对边分别相等的四边形是平行四边形 解:所画图形如图所示.

3.(答题模板)如图,四边形ABCD中,AB //CD,∠B=∠D.求证:四边形ABCD为平行四边形.
证明:∵AB//________,
∴∠B+__________ = 180°,
∠A+∠D=________,
∵________ =∠D,
∴∠C=________,
∴四边形ABCD为________________.
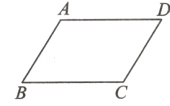
证明:∵AB//________,
∴∠B+__________ = 180°,
∠A+∠D=________,
∵________ =∠D,
∴∠C=________,
∴四边形ABCD为________________.

答案:
CD $\angle C$ $180^{\circ}$ $\angle B$ $\angle A$ 平行四边形
4.如图,点B,E,C,F在一条直线上,AB=DE,AC=DF,BE=CF.
(1)求证:△ABC≌△DEF;
(2)连接AD,求证:四边形ABED是平行四边形.
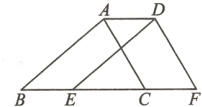
(1)求证:△ABC≌△DEF;
(2)连接AD,求证:四边形ABED是平行四边形.

答案:
(1)证明:$\because BE = CF$,$\therefore BE + EC = CF + EC$,即$BC = EF$.在$\triangle ABC$和$\triangle DEF$中,$\begin{cases}AB = DE,\\AC = DF,\\BC = EF,\end{cases}$$\therefore \triangle ABC\cong \triangle DEF(SSS)$.
(2)由
(1)知,$\triangle ABC\cong \triangle DEF$,$\therefore \angle B = \angle DEF$,$\therefore AB// DE$.又$\because AB = DE$,$\therefore$四边形$ABED$是平行四边形.
(1)证明:$\because BE = CF$,$\therefore BE + EC = CF + EC$,即$BC = EF$.在$\triangle ABC$和$\triangle DEF$中,$\begin{cases}AB = DE,\\AC = DF,\\BC = EF,\end{cases}$$\therefore \triangle ABC\cong \triangle DEF(SSS)$.
(2)由
(1)知,$\triangle ABC\cong \triangle DEF$,$\therefore \angle B = \angle DEF$,$\therefore AB// DE$.又$\because AB = DE$,$\therefore$四边形$ABED$是平行四边形.
5.如图,在四边形ABCD中,∠ACB =∠CAD=90°,点E在BC上,AE//DC,EF⊥AB,垂足为F.
(1)求证:四边形AECD是平行四边形;
(2)若AE平分∠BAC,BE=5,BF=4,求AD的长.
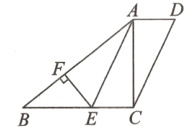
(1)求证:四边形AECD是平行四边形;
(2)若AE平分∠BAC,BE=5,BF=4,求AD的长.

答案:
(1)证明:$\because \angle ACB = \angle CAD = 90^{\circ}$,$\therefore AD// CE$.$\because AE// DC$,$\therefore$四边形$AECD$是平行四边形.
(2)解:在$Rt\triangle BEF$中,$\because BE = 5$,$BF = 4$.$\therefore EF = \sqrt{BE^{2}-BF^{2}}=\sqrt{5^{2}-4^{2}} = 3$.$\because AE$平分$\angle BAC$,$EF\perp AB$,$\angle ACE = 90^{\circ}$,$\therefore EC = EF = 3$.由
(1)得四边形$AECD$是平行四边形,$\therefore AD = EC = 3$.
(1)证明:$\because \angle ACB = \angle CAD = 90^{\circ}$,$\therefore AD// CE$.$\because AE// DC$,$\therefore$四边形$AECD$是平行四边形.
(2)解:在$Rt\triangle BEF$中,$\because BE = 5$,$BF = 4$.$\therefore EF = \sqrt{BE^{2}-BF^{2}}=\sqrt{5^{2}-4^{2}} = 3$.$\because AE$平分$\angle BAC$,$EF\perp AB$,$\angle ACE = 90^{\circ}$,$\therefore EC = EF = 3$.由
(1)得四边形$AECD$是平行四边形,$\therefore AD = EC = 3$.
查看更多完整答案,请扫码查看


