《2025年课堂点睛八年级数学下册人教版安徽专版》

1.(答题模板)如图,▱ABCD的对角线AC、BD交于点O.
(1)用尺规完成以下基本作图:过点O作AC的垂线分别交AB、DC于点E、F;
(不写作法,保留作图痕迹)
(2)在(1)问的条件下,连接AF、CE,求证:四边形AECF为菱形,并将下面的证明过程补充完整.
　　　　　　
证明:∵四边形ABCD是平行四边形,
∴AO=CO,______________.
∴∠FCO=∠EAO.
在△FOC和△EOA中,
$\begin{cases} \angle FCO=\angle EAO, \\ CO = AO, \\ \_\_\_\_\_\_\_\_, \end{cases}$
∴△FOC≌△EOA(ASA),
∴______________.∵AO=CO,
∴四边形AECF为平行四边形.
∵______________,
∴四边形AECF为菱形.

答案：

(1)解:如图
(2)$CD// AB$，$\angle COF = \angle AOE$，$OF = OE$，$AC\perp EF$

2.如图,已知四边形ABCD是平行四边形,点E,F分别是AB,BC上的点,AE=CF,并且∠AED=∠CFD.求证:

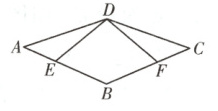
(1)△AED≌△CFD;
(2)四边形ABCD是菱形.

答案：
(1)证明:$\because$四边形$ABCD$是平行四边形，$\therefore\angle A=\angle C$. 又$\because AE = CF$，$\angle AED=\angle CFD$，$\therefore\triangle AED\cong\triangle CFD(ASA)$.
(2)$\because\triangle AED\cong\triangle CFD$，$\therefore AD = CD$. 又$\because$四边形$ABCD$是平行四边形，$\therefore$四边形$ABCD$是菱形.

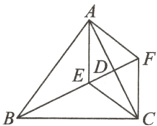
3.如图,在△ABC中,BA = BC,BD平分∠ABC交AC于点D,点E在线段BD上,点F在BD的延长线上,且DE=DF,连接AE,CE,AF,CF.
(1)求证:四边形AECF是菱形;
(2)若BA⊥AF,AD = 4,BC = 4$\sqrt{5}$,求BD和AE的长.
　　　　　　　　　　　　　　　　
　　　　　　　　　　　　　　　　

答案：
(1)证明:$\because BA = BC$，$BD$平分$\angle ABC$，$\therefore BD\perp AC$，$AD = CD$. $\because DE = DF$，$\therefore$四边形$AECF$是平行四边形，又$EF\perp AC$，$\therefore$四边形$AECF$是菱形.
(2)解:$\because AD\perp BD$，$AD = 4$，$BA = BC = 4\sqrt{5}$，$\therefore BD=\sqrt{AB^{2}-AD^{2}}=\sqrt{80 - 16}=8$. 设$DE = x$，则$DF = x$，$\therefore AF^{2}=AD^{2}+DF^{2}=16 + x^{2}$. $\because BF = BD + DF = 8 + x$，$BA\perp AF$，$\therefore AB^{2}+AF^{2}=BF^{2}$. $\therefore(4\sqrt{5})^{2}+16 + x^{2}=(8 + x)^{2}$. $\therefore x = 2$. $\therefore DE = DF = 2$. $\therefore AE=\sqrt{AD^{2}+DE^{2}}=\sqrt{4^{2}+2^{2}}=2\sqrt{5}$. $\therefore BD$和$AE$的长分别为$8$和$2\sqrt{5}$.