《2025年课堂点睛八年级数学下册人教版安徽专版》

1. 如图，在△ABC中，AB = 5，AC = 13，AD⊥AB交BC于点D，D为BC中点，求AD的长.
　　　　　　　　　　

答案： 解:延长AD至点E,使得AD=ED,连接CE,易证△ADB≌△EDC(SAS),
∴∠E=∠BAD=90°,CE=AB=5,
∴在Rt△AEC中,AE = √(13² - 5²) = 12,
∴AD = 6.

2. 如图，在Rt△ABC中，AB = 9，BC = 6，∠B = 90°，将△ABC折叠，使A点与BC的中点D重合，折痕为MN，求BN的长.
　　　　　　　　　　　

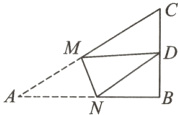
答案： 解:设BN=x,AN=ND=9 - x,BD = 1/2BC = 3,在Rt△BND中,x² + 3² = (9 - x)²,x = 4,
∴BN = 4.

3. 如图，将一个矩形纸片ABCD沿EF折叠，使B和D重合，若AB = 3，BC = 9. 求：
　(1)BE的长；
　(2)EF的长.
　　　　　　　　　

答案：
(1)解:设BE=x,在Rt△BAE中,3² + (9 - x)² = x²,x = 5,BE = 5.
(2)∠BFE = ∠FED = ∠BEF,
∴BE = BF = 5,作EM⊥BC交BF于M点,
∴FM = 1,在Rt△EMF中,EF = √10.

4. 如图，在边长为4的正方形纸片ABCD中，点P在边AD上，点Q在边AB上，AQ = 3，连接DQ、CP，DQ与CP交于点H，将正方形纸片ABCD沿CP折叠，点D的对应点D₁恰好落在DQ上.
　　　(1)求证：△CDP≌△DAQ；
　　　(2)求D₁Q的长.
　　　　　　　　　　　　　

答案：
(1)证明:
∵四边形ABCD是正方形,
∴∠CDP = ∠DAQ = 90°,由折叠的性质得DH = D₁H,D₁H⊥CP,
∴∠CHD = ∠DCP + ∠CDH = 90°,又
∵∠CDP = ∠ADQ + ∠CDH = 90°,
∴∠DCP = ∠ADQ,在△CDP和△DAQ中,{∠DCP = ∠ADQ, CD = DA, ∠CDP = ∠DAQ},
∴△CDP≌△DAQ(ASA).
(2)解:由
(1)得△CDP≌△DAQ,
∴DP = AQ = 3,CP = DQ,在Rt△DAQ中,由勾股定理得DQ = √(AD² + AQ²) = √(3² + 4²) = 5,
∴CP = DQ = 5,由1/2DC·DP = 1/2DH·CP,得DH = DC·DP/CP = 4×3/5 = 12/5,
∴DD₁ = 2DH = 24/5,
∴D₁Q = DQ - DD₁ = 5 - 24/5 = 1/5.