《2025年课堂点睛八年级数学下册人教版安徽专版》

1. 如图，在□ABCD中，对角线AC与BD相交于点O，且AC=10，BD=6，AB=4.
(1)求证：AB⊥BD；
(2)E，F分别是AD和BC的中点，连接BE，DF，求证：四边形BEDF是菱形.
　　　　　　　　

答案：
(1)证明:
∵在▱ABCD中，对角线AC与BD相交于点O,且AC=10,BD=6，
∴AO=CO=$\frac{1}{2}$AC=5,BO=DO=$\frac{1}{2}$BD=3.
∵AB²+BO²=4²+3²=25,AO²=5²=25,
∴AB²+BO²=AO².
∴△ABO为直角三角形,∠ABD=90°,
∴AB⊥BD.
(2)
∵四边形ABCD是平行四边形，
∴BC=AD,AB//CD.由
(1)可知△ABD 为直角三角形，
∴∠CDB=∠ABD=90°.
∵E,F分别是AD和BC的中点，
∴BE =DE=$\frac{1}{2}$AD,BF=DF=$\frac{1}{2}$BC.
∴BE=DE=BF=DF,
∴四边形BEDF是菱形.

2. 如图，边长为4的正方形ABCD的对角线的交点为O，另一个边长为4的正方形OEFG绕着点O转动，且边OE，OG分别交边BC，CD于点M，N.
(1)求证：△OBM≌△OCN.
(2)设这两个正方形的重叠部分的面积为S，则S是否为定值？若是，求出S的值；若不是，请说明理由.
　　　　　　　　　　　　　

答案：
(1)证明:
∵四边形ABCD和四边形OEFG都是正方形，
∴OB=OC,∠OBM=∠OCN=45°,∠BOC=∠EOG=90°.
∴∠BOC−∠MOC=∠EOG−∠MOC,即∠BOM=∠CON,
∴△OBM≌△OCN(ASA).
(2)解:S是定值.
∵△OBM≌△OCN,
∴S△OBM=S△OCN.
∴S△OCN+S△OCM=S△OBM+S△OCM,即S=S△OBC=$\frac{1}{4}$S正方形ABCD=$\frac{1}{4}$×4²=4,即重叠部分的面积S是定值，为4.

3. 如图，在四边形ABCD中，AD//BC，∠A=90°，AD=5，BC=13，E是边CD的中点，连接BE并延长交AD的延长线于点F，连接CF.
(1)求证：四边形BDFC是平行四边形；
(2)若BD=BC，求四边形BDFC的面积.
　　　　　　　　　　　　　

答案：
(1)证明:
∵AD//BC,
∴∠CBE=∠DFE.
∵E是边CD的中点，
∴CE=DE.又∠BEC =∠FED.
∴△BEC≌△FED(AAS),
∴BE=FE.
∴四边形BDFC是平行四边形.
(2)解:
∵BD=BC=13,∠A=90°,
∴AB=$\sqrt{BD²−AD²}$=$\sqrt{13²−5²}$=12.由
(1)得四边形BDFC是平行四边形，
∴S▱BDFC=BC·AB = 13×12 = 156.

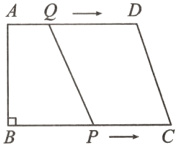
4. 如图，在四边形ABCD中，AD//BC，∠B=90°，AD=8cm，BC=10cm，AB=6cm，点Q从点A出发以1cm/s的速度向点D运动，点P从点B出发以2cm/s的速度向点C运动，P，Q两点同时出发，当点P到达点C时，掉头沿CB方向继续运动，直至点Q到达点D，两点同时停止运动.设运动时间为t s.
(1)直接写出：AQ=______cm，DQ=______cm；(用含t的式子表示)
(2)连接PQ，当t为何值时，四边形PQDC为平行四边形？请直接写出t的值.
　　　　　　　　　　　　　

答案：
(1)t　(8−t)
(2)解:当t = 2或6时，四边形PQDC为平行四边形.