搜索
13.在△ABC中,∠ABC=60°,AD为BC边上的高,AD=6√3,CD=1,则BC的长为________.
答案：
5或7
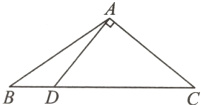
14.(10分)如图,在△ABC中,D是BC上一点,且AD⊥AC,AC=4,BC=7,AD=3,求BD的长.
答案：
解:
∵AD⊥AC,
∴∠DAC = 90°.在Rt△ACD中,由勾股定理,得CD² = AD² + AC² = 3² + 4² = 25,
∴CD = 5.
∵BC = 7,
∴BD = BC - CD = 7 - 5 = 2.
∵AD⊥AC,
∴∠DAC = 90°.在Rt△ACD中,由勾股定理,得CD² = AD² + AC² = 3² + 4² = 25,
∴CD = 5.
∵BC = 7,
∴BD = BC - CD = 7 - 5 = 2.
15.(10分)如图,在边长为1的正方形网格中,以格点为顶点作一个三边长分别为√5,√8,√17的三角形.
答案：
解:如图
,△ABC 即为所求.(画法不唯一)
解:如图
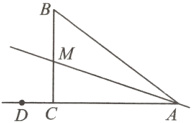
,△ABC 即为所求.(画法不唯一) 16.(11分)如图,在Rt△ABC中,∠ACB=90°,BC=3,AC=4,在边BC上有一点M,将△ABM沿直线AM折叠,点B恰好落在边AC延长线上的点D处.
(1)AB的长=______;
(2)CD的长=______;
(3)求CM的长.
(1)AB的长=______;
(2)CD的长=______;
(3)求CM的长.
答案：
(1)5
(2)1
(3)解:连接DM.
∵∠ACB = 90°,
∴∠DCM = 90°.设CM = x(x＞0),则DM = BM = 3 - x.在Rt△DCM中,根据勾股定理,得x² + 1² = (3 - x)²,解得x = $\frac{4}{3}$,即CM = $\frac{4}{3}$.
(1)5
(2)1
(3)解:连接DM.
∵∠ACB = 90°,
∴∠DCM = 90°.设CM = x(x＞0),则DM = BM = 3 - x.在Rt△DCM中,根据勾股定理,得x² + 1² = (3 - x)²,解得x = $\frac{4}{3}$,即CM = $\frac{4}{3}$.
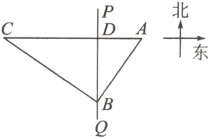
17.(12分)如图,南北方向PQ以东为我国领海,以西为公海,晚上10:28,我边防反偷渡巡逻101号艇在A处发现其正西方向的C处有一艘可疑船只正向我国领海靠近,便立即通知正在PQ上B处巡逻的103号艇注意其动向,经检测AC=10海里,AB=6海里,BC=8海里,若该可疑船只的速度为12.8海里,则该可疑船只最早何时进入我国领海?
答案：
解:
∵AB² + BC² = 6² + 8² = 100 = AC²,
∴△ABC为直角三角形，且∠ABC = 90°,又
∵S_{△ABC} = $\frac{1}{2}$AC·BD = $\frac{1}{2}$AB·BC,
∴$\frac{1}{2}$×10·BD = $\frac{1}{2}$×6×8,解得BD = 4.8.在Rt△BCD中,CD² = BC² - BD² = 8² - 4.8² = 40.96,
∴CD = 6.4,故该可疑船只从被发现到进入我国领海的最短航行时间为6.4÷12.8 = 0.5(h).因此该可疑船只最早进入我国领海的时间为晚上10:58.
∵AB² + BC² = 6² + 8² = 100 = AC²,
∴△ABC为直角三角形，且∠ABC = 90°,又
∵S_{△ABC} = $\frac{1}{2}$AC·BD = $\frac{1}{2}$AB·BC,
∴$\frac{1}{2}$×10·BD = $\frac{1}{2}$×6×8,解得BD = 4.8.在Rt△BCD中,CD² = BC² - BD² = 8² - 4.8² = 40.96,
∴CD = 6.4,故该可疑船只从被发现到进入我国领海的最短航行时间为6.4÷12.8 = 0.5(h).因此该可疑船只最早进入我国领海的时间为晚上10:58.
查看更多完整答案，请扫码查看
