《2025年课堂点睛八年级数学下册人教版安徽专版》

13. (8分)如图,在四边形ABCD中,AB=AD,BD平分∠ABC,∠A=∠C. 求证:四边形ABCD是菱形.

答案： 证明:
∵BD平分∠ABC,
∴∠ABD = ∠CBD.又∠A = ∠C,BD = BD,
∴△ABD ≌△CBD(AAS).
∴AB = BC,AD = CD.又AB = AD,
∴AB = BC = CD = AD.
∴四边形ABCD是菱形.

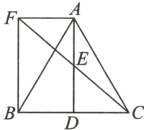
14. (10分)如图,在△ABC中,D是BC的中点,E是AD的中点,过点A作AF//BC交CE的延长线于点F.
(1)求证:AF=BD;(5分)
(2)连接BF,若AB=AC,求证:四边形ADBF是矩形.(5分)

答案：
(1)证明:
∵AF//BC,
∴∠AFE = ∠DCE,∠FAE = ∠CDE.又
∵E为AD的中点，
∴AE = DE.
∴△AEF≌△DEC(AAS).
∴AF = DC.又
∵D为BC的中点，
∴BD = CD.
∴AF = BD;　　
(2)
∵AF = BD,AF//BD,
∴四边形ADBF是平行四边形.
∵AB = AC,D为BC的中点，
∴AD⊥BC.
∴∠ADB = 90°.
∴平行四边形ADBF是矩形.

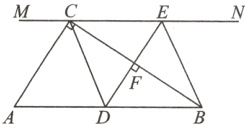
15. (12分)如图,在Rt△ABC中,∠ACB = 90°,过点C的直线MN//AB,D为AB边上一点,过点D作DE⊥BC,交直线MN于点E,垂足为F,连接CD,BE.
(1)若AD=4cm,则CE的长是______cm;(2分)
(2)当点D为AB的中点时,四边形BECD是什么特殊四边形? 说明你的理由;(5分)
(3)若点D为AB的中点,当∠A的大小满足什么条件时,四边形BECD是正方形? 并说明理由.(5分)

答案：
(1)4　
(2)解:四边形BECD是菱形.理由如下:由
(1),得CE = AD,
∵∠ACB = 90°,点D为AB的中点，
∴AD = BD = CD.
∴BD = CE.
∵BD//CE,
∴四边形BECD是平行四边形.
∵CD = BD,
∴四边形BECD是菱形;　
(3)当∠A = 45°时，四边形BECD是正方形.理由如下:
∵∠ACB = 90°,∠A = 45°,
∴∠ABC = 45°.又
∵点D为AB的中点，
∴CD = BD = AD.
∴∠DCB = ∠DBC = 45°.
∴∠CDB = 90°.又
∵四边形BECD是菱形，
∴四边形BECD是正方形.