1. 下列式子中,一定是二次根式的是( )
A. $\sqrt{-2025}$
B. $\sqrt{8}$
C. $\sqrt[3]{2}$
D. $\sqrt{a}$
A. $\sqrt{-2025}$
B. $\sqrt{8}$
C. $\sqrt[3]{2}$
D. $\sqrt{a}$
答案:
1.B
2. 若式子$\frac{\sqrt{x}}{x - 2}$有意义,则实数$x$的取值范围是( )
A. $x\neq2$
B. $x\geqslant0$
C. $x\geqslant2$
D. $x\geqslant0$且$x\neq2$
A. $x\neq2$
B. $x\geqslant0$
C. $x\geqslant2$
D. $x\geqslant0$且$x\neq2$
答案:
2.D
3. 实数$a$在数轴上的位置如图所示,则式子$\sqrt{(a - 4)^2}-\sqrt{(a - 11)^2}$化简后的结果为( )
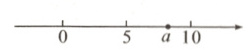
A. 7
B. -7
C. $15 - 2a$
D. $2a - 15$
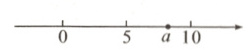
A. 7
B. -7
C. $15 - 2a$
D. $2a - 15$
答案:
3.D
4. 若$a + |a| = 0$,则$\sqrt{(a - 2)^2}+\sqrt{a^2}=$( )
A. $2 - 2a$
B. $2a - 2$
C. -2
D. 2
A. $2 - 2a$
B. $2a - 2$
C. -2
D. 2
答案:
4.A
5. 计算$(\sqrt{5})^2 =$______.
答案:
5.5
6. 若$(a - 3)^2+|b + 1|^2 = 0$,则$a - b =$______.
答案:
6.4
7. 若一个长方形的面积为$10\text{cm}^2$,它的长与宽的比为$5:1$,则它的长为______cm,宽为______cm.
答案:
7.5√2 √2
8. 若$\sqrt{8 - x}$为整数,$x$为正整数,则$x$的值是__________.
答案:
8.4或7或8
9. (8分)计算:
(1)$\sqrt{5^2}-(-\sqrt{6})^2$;
(2)$(\sqrt{3})^2-\sqrt{(-3)^2}+3\sqrt{(-\frac{1}{3})^2}$.
(1)$\sqrt{5^2}-(-\sqrt{6})^2$;
(2)$(\sqrt{3})^2-\sqrt{(-3)^2}+3\sqrt{(-\frac{1}{3})^2}$.
答案:
9.
(1)解:原式=5 - 6 = - 1.
(2)解:原式=3 - 3 + 3×$\frac{1}{3}$=1.
(1)解:原式=5 - 6 = - 1.
(2)解:原式=3 - 3 + 3×$\frac{1}{3}$=1.
10. (10分)(1)若$-4\leqslant x\leqslant3$,化简$\sqrt{x^2 + 8x + 16}-\sqrt{x^2 - 6x + 9}$;(5分)
(2)若化简$|1 - a|-\sqrt{a^2 - 8a + 16}$的结果是$2a - 5$,求实数$a$的取值范围.(5分)
(2)若化简$|1 - a|-\sqrt{a^2 - 8a + 16}$的结果是$2a - 5$,求实数$a$的取值范围.(5分)
答案:
10.
(1)解:原式=$\sqrt{(x + 4)^2}-\sqrt{(x - 3)^2}$.
∵ - 4≤x≤3,
∴x + 4≥0,x - 3≤0.
∴原式=x + 4 + x - 3 = 2x + 1.
(2)
∵|1 - a|-$\sqrt{a^2 - 8a + 16}$=|1 - a|-|a - 4|=2a - 5,
∴应该满足|1 - a|-|a - 4|=(a - 1)-(4 - a).
∴$\begin{cases}a - 1\geq0\\4 - a\geq0\end{cases}$.
∴1≤a≤4.
(1)解:原式=$\sqrt{(x + 4)^2}-\sqrt{(x - 3)^2}$.
∵ - 4≤x≤3,
∴x + 4≥0,x - 3≤0.
∴原式=x + 4 + x - 3 = 2x + 1.
(2)
∵|1 - a|-$\sqrt{a^2 - 8a + 16}$=|1 - a|-|a - 4|=2a - 5,
∴应该满足|1 - a|-|a - 4|=(a - 1)-(4 - a).
∴$\begin{cases}a - 1\geq0\\4 - a\geq0\end{cases}$.
∴1≤a≤4.
查看更多完整答案,请扫码查看


