《2025年53精准练八年级数学下册华师大版山西专版》

9.[2023晋中榆次区期末]如图是一支温度计的示意图，图中左边是用摄氏温度表示的温度值，右边是用华氏温度表示的温度值，这两个温度之间的部分对应关系如下表：

|摄氏温度$x/^{\circ}C$|0|10|20|30|40|50|
|----|----|----|----|----|----|----|
|华氏温度$y/^{\circ}F$|32|50|68|86|104|122|
根据表中信息，可得y与x之间的表达式为( )


A. $y = \frac{9}{5}x + 32$
B. $y = x + 32$
C. $y = x + 40$
D. $y = \frac{5}{9}x + 32$

答案： A

10.[真实情境问题]如图，规定大拇指与小拇指尽量张开时，两指尖的距离记为d.研究表明，身高h与两指尖的距离d之间近似满足一次函数关系：$h = kd - 20$，现测量得$d = 20$ cm，$h = 160$ cm，若$d = 22$ cm，则$h =$（ ）


A. 168 cm
B. 173 cm
C. 178 cm
D. 182 cm

答案： C

11.[数形结合]如图，在平面直角坐标系中，直线$y = - \frac{3}{4}x + 3$交x轴于点A，交y轴于点B，以点A为圆心，AB长为半径画弧，交x轴的负半轴于点C，则直线BC的表达式为（ ）

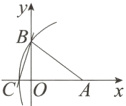
A. $y = 3x + 3$
B. $y = 4x + 3$
C. $y = 4x + 4$
D. $y = - 4x + 4$

答案： A

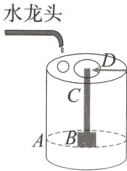
12.[2023晋中榆次区期末]在“制作计时器”项目式学习中，小明利用古代漏壶的原理制作如下计时器模型：A是一个高为60 cm的圆柱形玻璃容器，B是用塑料制作的底托，C为轻质塑料标尺，D为固定于容器盖口处的指示箭头.将水龙头调至匀速滴水状态，经过2小时，标尺显示底托高度由0 cm上升到12 cm，其中标尺显示底托的高度y(cm)是滴水时间x(小时)的正比例函数.
(1)求y与x之间的函数表达式；
(2)该装置最多可计时多长时间?

答案： 解:
(1)设y与x之间的函数表达式为y = kx，将x = 2，y = 12代入得12 = 2k，解得k = 6，所以y与x之间的函数表达式为y = 6x.
(2)将y = 60代入y = 6x，得60 = 6x，解得x = 10，所以该装置最多可计时10小时.

13.[几何直观]已知一次函数$y = kx + b$的图象经过点A(2，3)与点B(0，5).
(1)求此一次函数的表达式；
(2)若点P为此一次函数图象上一点，且$\triangle POB$的面积为10，求点P的坐标.
思路点拨：(2)设点P的坐标，并用点P的横坐标表示出$\triangle POB$的面积.

答案： 解:
(1)因为一次函数的图象经过点A(2,3)，B(0,5)，所以2k + b = 3，b = 5，所以k = -1，所以一次函数的表达式为y = -x + 5.
(2)设点P坐标为(a,-a + 5)，因为B(0,5)，所以OB = 5.因为$S_{\triangle POB}=10$，所以$\frac{1}{2}\times5\times|a| = 10$，所以a = ±4，所以P点坐标为(4,1)或(-4,9).