《2025年53精准练八年级数学下册华师大版山西专版》

10. 图中三角形是有规律地从里到外逐层排列的，设$y$为第$n$层($n$为正整数)三角形的个数，则下列函数关系式中正确的是 （ ）

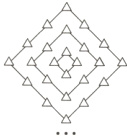
A. $y = 4n - 4$
B. $y = 4n$
C. $y = 4n + 4$
D. $y = n^{2}$

答案： B

11. 若$y - 3$是$x$的正比例函数，则$y$是$x$的 （ ）
A. 正比例函数
B. 一次函数，但不是正比例函数
C. 函数，但不是一次函数
D. 不存在函数关系

答案： B

12. [2023晋中榆次区期中]爱思考的小颖同学学习了函数之后发现，物理、生物、地理的学习中也有许多函数，例如下面的一些情形，其中变量$y$不是$x$的正比例函数的是 （ ）
A. 汽车以60 km/h的速度匀速行驶，行驶路程$y$(km)与行驶时间$x$(h)
B. 某同学利用回声测距，他对着山崖喊话，喊出后经过$x$(s)听到回声，山崖与他相距$y$(m)(声音在空气中的传播速度取340 m/s)
C. 一棵树现在高50 cm，每个月长高2 cm，$x$个月后这棵树的高度为$y$ cm
D. 在一幅比例尺为1 : 27 000 000的地图上，图上距离$y$(cm)与实际距离$x$(km)

答案： C

13. 如图，$\triangle ABC$的边$BC$的长是10，$BC$边上的高是6，点$D$在边$BC$上运动(点$D$不与点$B$，$C$重合).设$BD$的长为$x$，则$\triangle ACD$的面积$y$与$x$之间的函数关系式为____________________，自变量$x$的取值范围是______________.

答案： $y = - 3x + 30$; $0\lt x\lt10$

14. 某剧院的观众席的座位为扇形，且按下列方式设置：
|排数$x$|1|2|3|4|…|
|----|----|----|----|----|----|
|座位数$y$|50|53|56|59|…|
(1)按照上表所示的规律，当排数为6时，座位数为多少?
(2)写出座位数$y$与排数$x$之间的关系式.
(3)按照上表所示的规律，某一排可能有90个座位吗? 请说明理由.

答案： 解:
(1) 由题表可知, 第$5$排座位比第$4$排多$3$个, 第$6$排座位比第$5$排多$3$个, 故当排数为$6$时, 座位数为$65$.
(2) 从第$2$排开始, 每一排比它前面一排多$3$个座位, 则第$x$排比第$1$排多$3(x - 1)$个座位, 从而得到$y$与$x$的关系式为$y = 50+3(x - 1)$, 即$y = 3x + 47$.
(3) 不可能. 理由如下:
当$y = 90$时, $3x + 47 = 90$,
解得$x=\frac{43}{3}$,
因为$\frac{43}{3}$不是正整数,
所以某一排不可能有$90$个座位.

15. [真实情境问题]某超市为了促进消费，推出“会员日”活动.方案一：花费100元购买会员卡，当天所有商品享受八折；方案二：不购买会员卡，商品一律打九折.
(1)用$x$(元)表示会员日购买的商品原价，用$y$(元)表示实际支付金额，请写出这两种购买方案中$y$与$x$之间的函数关系式.
(2)若某位消费者选择购买会员卡，他所购买商品的原价为280元，则实际应支付多少元?
(3)在支出预算为400元的情况下，选择哪种方案更划算?
(4)在实际支出为多少元的情况下，选择两种方案没有差别?

答案： 解:
(1) 方案一: $y = 100 + 0.8x$;
方案二: $y = 0.9x$.
(2) 由
(1)可知, 若购买会员卡进行支付, 则实际应支付$100 + 0.8\times280 = 324$(元).
(3) 令$100 + 0.8x = 400$, 解得$x = 375$,
令$0.9x = 400$, 解得$x=\frac{4000}{9}$.
因为$\frac{4000}{9}\gt375$,
所以在支出预算为$400$元的情况下, 选择方案二更划算.
(4) 令$100 + 0.8x = 0.9x$,
解得$x = 1000$,
所以在实际支出为$1000$元时, 选择两种方案没有差别.