2025年世纪金榜金榜学案八年级数学下册人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年世纪金榜金榜学案八年级数学下册人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第58页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
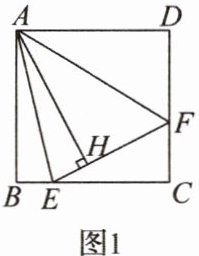
1. 如图1,在正方形ABCD内作∠EAF = 45°,AE交BC于点E,AF交CD于点F,连接EF,过点A作AH⊥EF,垂足为H.
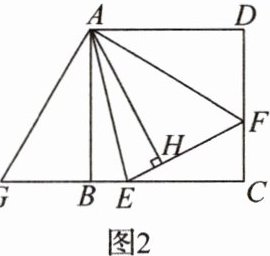
(1)如图2,将△ADF绕点A顺时针旋转90°得到△ABG.
①求证:△AGE≌△AFE;
②若BE = 2,DF = 3,求AH的长.
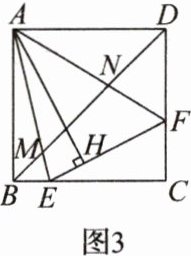
(2)如图3,连接BD交AE于点M,交AF于点N. 请探究并猜想:线段BM,MN,ND之间有什么数量关系?并说明理由.
(1)如图2,将△ADF绕点A顺时针旋转90°得到△ABG.
①求证:△AGE≌△AFE;
②若BE = 2,DF = 3,求AH的长.
(2)如图3,连接BD交AE于点M,交AF于点N. 请探究并猜想:线段BM,MN,ND之间有什么数量关系?并说明理由.



答案:
【解析】
(1)①由旋转的性质可知,AF = AG,∠DAF = ∠BAG。 因为四边形ABCD为正方形,所以∠BAD = 90°。又因为∠EAF = 45°,所以∠BAE + ∠DAF = 45°,进而∠BAG + ∠BAE = 45°,即∠GAE = ∠FAE。 在△GAE和△FAE中, \[ \begin{cases} AG = AF \\ \angle GAE = \angle FAE \\ AE = AE \end{cases} \] 所以△GAE≌△FAE(SAS)。 ②因为△GAE≌△FAE,AB⊥GE,AH⊥EF,所以AB = AH,GE = EF = 5。 设正方形的边长为x,则EC = x - 2,FC = x - 3。 在Rt△EFC中,由勾股定理得EF² = FC² + EC²,即(x - 2)² + (x - 3)² = 25。 解得x = 6。所以AB = 6,AH = 6。
(2)如图所示,将△ABM逆时针旋转90°得△ADM'。 因为四边形ABCD为正方形,所以∠ABD = ∠ADB = 45°。
由旋转的性质可知,∠ABM = ∠ADM' = 45°,BM = DM'。
所以∠NDM' = 90°。
在Rt△NM'D中根据勾股定理得NM'² = ND² + DM'²。
因为∠EAM' = 90°,∠EAF = 45°,所以∠EAF = ∠FAM' = 45°。
在△AMN和△AM'N中,
\[
\begin{cases}
AM = AM' \\
\angle MAN = \angle M'AN \\
AN = AN
\end{cases}
\]
所以△AMN≌△AM'N(SAS)。
所以MN = M'N。又因为BM = DM',所以MN² = ND² + BM²。
因为四边形ABCD为正方形,所以∠ABD = ∠ADB = 45°。
由旋转的性质可知,∠ABM = ∠ADM' = 45°,BM = DM'。
所以∠NDM' = 90°。
在Rt△NM'D中根据勾股定理得NM'² = ND² + DM'²。
因为∠EAM' = 90°,∠EAF = 45°,所以∠EAF = ∠FAM' = 45°。
在△AMN和△AM'N中,
\[
\begin{cases}
AM = AM' \\
\angle MAN = \angle M'AN \\
AN = AN
\end{cases}
\]
所以△AMN≌△AM'N(SAS)。
所以MN = M'N。又因为BM = DM',所以MN² = ND² + BM²。
【解析】
(1)①由旋转的性质可知,AF = AG,∠DAF = ∠BAG。 因为四边形ABCD为正方形,所以∠BAD = 90°。又因为∠EAF = 45°,所以∠BAE + ∠DAF = 45°,进而∠BAG + ∠BAE = 45°,即∠GAE = ∠FAE。 在△GAE和△FAE中, \[ \begin{cases} AG = AF \\ \angle GAE = \angle FAE \\ AE = AE \end{cases} \] 所以△GAE≌△FAE(SAS)。 ②因为△GAE≌△FAE,AB⊥GE,AH⊥EF,所以AB = AH,GE = EF = 5。 设正方形的边长为x,则EC = x - 2,FC = x - 3。 在Rt△EFC中,由勾股定理得EF² = FC² + EC²,即(x - 2)² + (x - 3)² = 25。 解得x = 6。所以AB = 6,AH = 6。
(2)如图所示,将△ABM逆时针旋转90°得△ADM'。
 因为四边形ABCD为正方形,所以∠ABD = ∠ADB = 45°。
由旋转的性质可知,∠ABM = ∠ADM' = 45°,BM = DM'。
所以∠NDM' = 90°。
在Rt△NM'D中根据勾股定理得NM'² = ND² + DM'²。
因为∠EAM' = 90°,∠EAF = 45°,所以∠EAF = ∠FAM' = 45°。
在△AMN和△AM'N中,
\[
\begin{cases}
AM = AM' \\
\angle MAN = \angle M'AN \\
AN = AN
\end{cases}
\]
所以△AMN≌△AM'N(SAS)。
所以MN = M'N。又因为BM = DM',所以MN² = ND² + BM²。
因为四边形ABCD为正方形,所以∠ABD = ∠ADB = 45°。
由旋转的性质可知,∠ABM = ∠ADM' = 45°,BM = DM'。
所以∠NDM' = 90°。
在Rt△NM'D中根据勾股定理得NM'² = ND² + DM'²。
因为∠EAM' = 90°,∠EAF = 45°,所以∠EAF = ∠FAM' = 45°。
在△AMN和△AM'N中,
\[
\begin{cases}
AM = AM' \\
\angle MAN = \angle M'AN \\
AN = AN
\end{cases}
\]
所以△AMN≌△AM'N(SAS)。
所以MN = M'N。又因为BM = DM',所以MN² = ND² + BM²。 2.【方法回顾】
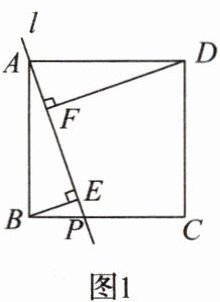
如图1,过正方形ABCD的顶点A作一条直线l交边BC于点P,BE⊥AP于点E,DF⊥AP于点F,猜想BE,DF,EF三条线段的数量关系:______________,并证明你的猜想.
【问题解决】
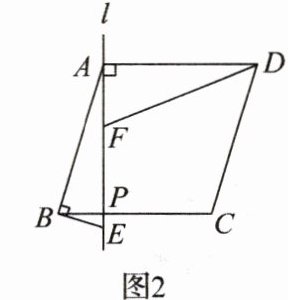
如图2,菱形ABCD的边长为\frac{3}{2},过点A作一条直线l交边BC于点P,且∠DAP = 90°,点F是AP上一点,且∠BAD + ∠AFD = 180°,过点B作BE⊥AB,与直线l交于点E,若EF = 1,求BE的长.
如图1,过正方形ABCD的顶点A作一条直线l交边BC于点P,BE⊥AP于点E,DF⊥AP于点F,猜想BE,DF,EF三条线段的数量关系:______________,并证明你的猜想.


【问题解决】
如图2,菱形ABCD的边长为\frac{3}{2},过点A作一条直线l交边BC于点P,且∠DAP = 90°,点F是AP上一点,且∠BAD + ∠AFD = 180°,过点B作BE⊥AB,与直线l交于点E,若EF = 1,求BE的长.
答案:
【解析】【方法回顾】DF - BE = EF。
证明:因为四边形ABCD是正方形,所以AB = AD,∠BAD = 90°。
因为∠BAE + ∠DAF = 90°,∠BAE + ∠ABE = 90°,所以∠ABE = ∠DAF。
又因为∠AFD = ∠BEA = 90°,所以△ABE≌△DAF(AAS)。
所以BE = AF,AE = DF,因为EF = AE - AF,所以DF - BE = EF。
【问题解决】
因为四边形ABCD为菱形,所以AB = AD。
因为BE⊥AB,所以∠ABE = ∠DAF = 90°。
因为∠BAD + ∠AFD = 180°,所以∠BAP + ∠FAD + ∠AFD = 180°。
又因为∠ADF + ∠FAD + ∠AFD = 180°,所以∠BAP = ∠ADF。
所以△ABE≌△DAF(ASA)。
所以DF = AE = AF + EF = AF + 1,AF = BE。
因为∠DAF = 90°,所以AF² + AD² = DF²。
即AF² + ($\frac{3}{2}$)²=(AF + 1)²。
解得AF=$\frac{5}{8}$,所以BE = AF=$\frac{5}{8}$。
查看更多完整答案,请扫码查看


