《2025年世纪金榜金榜学案八年级数学下册人教版》

6. 如图，圆柱形玻璃杯，高为14 cm，底面周长为16 cm，在杯内离杯底3 cm的点C处有一滴蜂蜜，此时一只蚂蚁正好在外壁，离杯上沿4 cm与蜂蜜相对的点A处，则蚂蚁到达蜂蜜的最短路程为________cm.

答案： 17

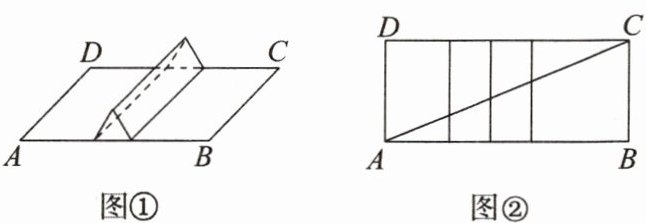
7. 问题情境：如图①，一只蚂蚁在一个长为100 cm，宽为50 cm的长方形地毯上爬行，地毯上堆放着一根正三棱柱木块，它的侧棱平行且等于宽AD，木块从正面看是一个边长为20 cm的等边三角形，求一只蚂蚁从点A处到达点C处需要走的最短路程.
数学抽象：将蚂蚁爬行过的木块的侧面“拉直”“铺平”“化曲为直”，连接AC.
（1）线段AC的长即蚂蚁从点A处到达点C处需要走的最短路程，依据是________________；
（2）问题解决：求出这只蚂蚁从点A处到达点C处需要走的最短路程.

答案： 【解析】
(1)线段AC的长即蚂蚁从点A处到达点C处需要走的最短路程，依据是两点之间线段最短； 答案：两点之间线段最短
(2)根据题意可得：展开图中的AB = 100 + 20 = 120(cm)，BC = 50 cm. 在Rt△ABC中，由勾股定理可得：AC = √(AB² + BC²)=√(120² + 50²)= 130(cm)，即这只蚂蚁从点A处到达点C处需要走的最短路程为130 cm.

8.【课本再现】
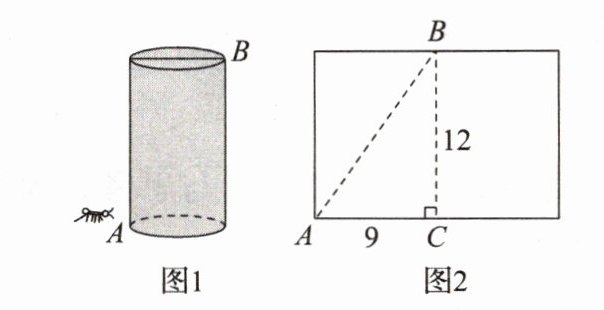
如图1，有一个圆柱，它的高为12 cm，底面圆的周长为18 cm. 在圆柱下底面的点A处有一只蚂蚁，它想吃到上底面与点A相对的点B处的食物，蚂蚁沿圆柱侧面爬行的最短路程是多少？

【方法探究】

(1)对于立体图形中求最短路程问题，应把立体图形展开成平面图形，再确定A，B两点的位置，依据“两点之间线段最短”，结合勾股定理，解决相应的问题. 如图2，在圆柱的侧面展开图中，点A，B对应的位置如图所示，利用勾股定理求出蚂蚁爬行的最短路程是__________cm.

【方法应用】

(2)如图3，直四棱柱的上下底面是正方形，底面边长为3 cm，高为10 cm. 在其侧面从点A开始，绕侧面两周，嵌入装饰彩条至点B停止. 求彩条的最短长度. 

(3)如图4，圆柱形玻璃杯底面周长为30 cm，高为35 cm，杯底厚1 cm. 在玻璃杯外壁距杯口2 cm的点A处有一只蚂蚁，蚂蚁相对面的内壁底部B处有一滴蜂蜜，蚂蚁沿杯口爬入内壁去吃蜂蜜，求蚂蚁爬行的最短路径长.(玻璃杯的壁厚忽略不计) 

答案：
【解析】
(1)根据题意得出：蚂蚁沿圆柱侧面爬行的最短路程是指展开后线段AB的长，由题意得：AC = 9 cm，BC = 12 cm. 在Rt△ABC中，由勾股定理得：AB = √(AC² + BC²)=√(9² + 12²)= 15(cm)，所以蚂蚁沿圆柱侧面爬行的最短路程是15 cm. 答案：15
(2)如图所示，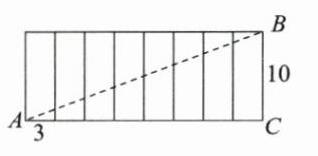
 
∵从点A开始经过4个侧面缠绕2圈到达点B，
∴展开后AC = 3×8 = 24(cm)，BC = 10 cm， 由勾股定理得：AB = √(AC² + BC²)=√(24² + 10²)= 26(cm)，所以彩条的最短长度是26 cm.
(3)展开玻璃杯的侧面，如图，作点A关于MN的对称点A'，连接A'B，作BC⊥A'A于点C，则BC = 15 cm，A'M = AM = 2 cm，CM = 35 - 1 = 34(cm)，CA' = CM + A'M = 36 cm. 在Rt△A'BC中，A'B = √(BC² + CA'²)=√(15² + 36²)= 39(cm)，所以蚂蚁爬行的最短路径长为39 cm.