《2025年世纪金榜金榜学案八年级数学下册人教版》

1.（2024·湖南中考）计算$\sqrt{2} \times \sqrt{7}$的结果是（ ）
A. $2\sqrt{7}$
B. $7\sqrt{2}$
C. 14
D. $\sqrt{14}$

答案： D

2.（2024·重庆中考）已知$m = \sqrt{27} - \sqrt{3}$，则实数$m$的取值范围是（ ）
A. $2 ＜ m ＜ 3$
B. $3 ＜ m ＜ 4$
C. $4 ＜ m ＜ 5$
D. $5 ＜ m ＜ 6$

答案： B

3.（2024·包头中考）计算$\sqrt{9^{2} - 6^{2}}$所得结果是（ ）
A. 3
B. $\sqrt{6}$
C. $3\sqrt{5}$
D. $\pm 3\sqrt{5}$

答案： C

4.（2024·安徽中考）我国古代数学家张衡将圆周率取值为$\sqrt{10}$，祖冲之给出圆周率的一种分数形式的近似值为$\frac{22}{7}$.比较大小：$\sqrt{10}$____$\frac{22}{7}$（填“＞”或“＜”）.

答案： ＞

5.（2024·威海中考）计算：$\sqrt{12} - \sqrt{8} \times \sqrt{6} =$______.

答案： -2√3

6.（2023·大连中考）下列计算正确的是（ ）
A. $(\sqrt{2})^{0} = \sqrt{2}$
B. $2\sqrt{3} + 3\sqrt{3} = 5\sqrt{6}$
C. $\sqrt{8} = 4\sqrt{2}$
D. $\sqrt{3}(2\sqrt{3} - 2) = 6 - 2\sqrt{3}$

答案： D

7.（2023·荆州中考）已知$k = \sqrt{2}(\sqrt{5} + \sqrt{3}) \cdot (\sqrt{5} - \sqrt{3})$，则与$k$最接近的整数为（ ）
A. 2
B. 3
C. 4
D. 5

答案： B

8.（2023·河北中考）若$a = \sqrt{2}$，$b = \sqrt{7}$，则$\sqrt{\frac{14a^{2}}{b^{2}}} =$（ ）
A. 2
B. 4
C. $\sqrt{7}$
D. $\sqrt{2}$

答案： A

9.（2024·盐城中考）长方形相邻两边长分别为$\sqrt{2}\text{ cm}$，$\sqrt{5}\text{ cm}$，设其面积为$S\text{ cm}^{2}$，则$S$在哪两个连续整数之间（ ）
A. 1和2
B. 2和3
C. 3和4
D. 4和5

答案： C

10.（2023·哈尔滨中考）计算$\sqrt{63} - 7\sqrt{\frac{1}{7}}$的结果是______.

答案： 2√7

11.（2023·呼伦贝尔中考）实数$m$在数轴上对应点的位置如图所示，化简：$\sqrt{(m - 2)^{2}} =$______.

答案： 2 - m

12.（2023·黄冈中考）请写出一个正整数$m$的值使得$\sqrt{8m}$是整数，$m =$______.

答案： 2（答案不唯一）

13.（2022·遂宁中考）实数$a$，$b$在数轴上的位置如图所示，化简$\vert a + 1\vert - \sqrt{(b - 1)^{2}} + \sqrt{(a - b)^{2}} =$______.

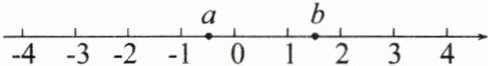
答案： 2

14.（2023·呼伦贝尔中考）观察下列各式：
$S_{1} = \sqrt{1 + \frac{1}{1^{2}} + \frac{1}{2^{2}}} = 1 + \frac{1}{1\times2}$，
$S_{2} = \sqrt{1 + \frac{1}{2^{2}} + \frac{1}{3^{2}}} = 1 + \frac{1}{2\times3}$，
$S_{3} = \sqrt{1 + \frac{1}{3^{2}} + \frac{1}{4^{2}}} = 1 + \frac{1}{3\times4}$，…
请利用你所发现的规律，计算：$S_{1} + S_{2} + \cdots + S_{50} =$______.

答案： 50 50/51