《2025年世纪金榜金榜学案八年级数学下册人教版》

1.（2024·珠海期中）如图，矩形ABCD沿着EF进行折叠，使点B落在边AD上的点B'处，点A落在点A'处.∠BFE = 55°，则∠DB'F的度数是（ ）

A. 100°
B. 110°
C. 120°
D. 130°

答案： B

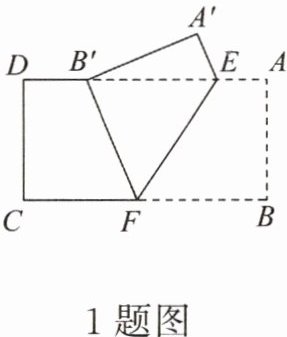
2.（2024·合肥期中）如图，在矩形纸片中，CD = 2，点E在AB上，将△BCE沿直线CE折叠.点B的对称点B'落在AD上时，∠B'CE = 22.5°，则∠AEB' = ______°.

答案： 45

3. 如图，矩形纸片ABCD中，AB = 8，AD = 6，折叠纸片使AD边落在对角线BD上，点A落在点A'处，折痕为DG，则AG的长为（ ）

A. 3
B. 4
C. 5
D. 6

答案： A

4.（2023·西宁中考）折叠问题是我们常见的数学问题，它是利用图形变化的轴对称性质解决的相关问题.数学活动课上，同学们以“矩形的折叠”为主题开展了数学活动.
矩形巧解折叠问题
【操作】如图1，在矩形ABCD中，点M在边AD上，将矩形纸片ABCD沿MC所在的直线折叠，使点D落在点D'处，MD'与BC交于点N.

【猜想】MN = CN
【验证】请将下列证明过程补充完整：
∵矩形纸片ABCD沿MC所在的直线折叠，
∴∠CMD = ______，
∵四边形ABCD是矩形，
∴AD//BC（矩形的对边平行），
∴∠CMD = ______（______），
∴______ = ______（等量代换），
∴MN = CN（______）.
【应用】
如图2，继续将矩形纸片ABCD折叠，使AM恰好落在MD'上，点A落在点A'处，点B落在点B'处，折痕为ME.
(1)猜想MN与EC的数量关系，并说明理由；
(2)若CD = 2，MD = 4，求EC的长.

答案： 【解析】【验证】因为矩形纸片ABCD沿MC所在的直线折叠，所以∠CMD = ∠CMD'，因为四边形ABCD是矩形，所以AD//BC（矩形的对边平行），所以∠CMD = ∠MCN（两直线平行，内错角相等），所以∠CMD' = ∠MCN（等量代换），所以MN = CN（等角对等边）； 【应用】
(1) EC = 2MN，理由如下：因为由四边形ABEM折叠得到四边形A'B'EM，所以∠AME = ∠A'ME，因为四边形ABCD是矩形，所以AD//BC（矩形的对边平行），所以∠AME = ∠MEN（两直线平行，内错角相等），所以∠A'ME = ∠MEN，所以MN = EN（等角对等边），因为MN = CN，所以MN = EN = NC，即EC = 2MN；
(2) 因为矩形ABCD沿MC所在直线折叠，所以∠D = ∠D' = 90°，DC = D'C = 2，MD = MD' = 4. 设MN = NC = x，则ND' = MD' - MN = 4 - x，在Rt△ND'C中，∠D' = 90°，由勾股定理得ND'² + D'C² = NC²，所以(4 - x)² + 2² = x²，解得x = $\frac{5}{2}$，所以EC = 2MN = 5.