《2025年海淀单元测试AB卷六年级数学下册苏教版》

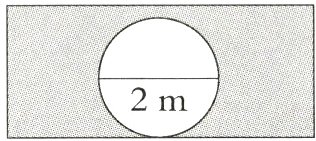
3. [新情境]张爷爷打算在菜地的周围修一道围墙，原计划用土石80 m³，后来又开了一个厚度是30 cm，直径是2 m的圆形门(如图)，减少了土石的用量。实际用了多少立方米的土石？(6分)

答案： 30 cm = 0.3 m
80 - 3.14×(2÷2)²×0.3 = 79.058(m³)
答：实际用了79.058 m³的土石。

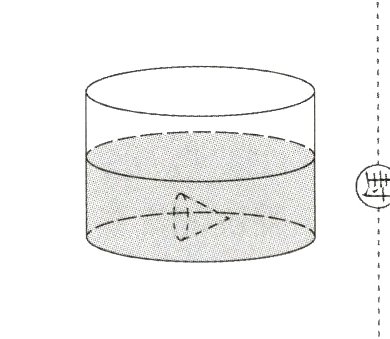
4. 如图所示的玻璃容器，从里面量，底面直径为12 cm，它的里面装有一部分水，水中浸没着一个高9 cm的圆锥形铅锤。当铅锤从水中取出后(水无溢出)，水面下降了0.5 cm。这个圆锥形铅锤的底面积是多少平方厘米？(6分)

答案： 3.14×($\frac{12}{2}$)²×0.5÷($\frac{1}{3}$×9) = 18.84(cm²)
答：这个圆锥形铅锤的底面积是18.84 cm²。
[解析]当铅锤取出时，水面下降的水的体积就是铅锤的体积，即3.14×(12÷2)²×0.5 = 56.52(cm³)。再根据圆锥形铅锤的高，求出圆锥形铅锤的底面积，即56.52÷9÷$\frac{1}{3}$=18.84(cm²)。

[辨思维]如图，小军和小红分别以直角梯形的上底和下底所在直线为轴，将直角梯形旋转一周，得到两个立体图形。

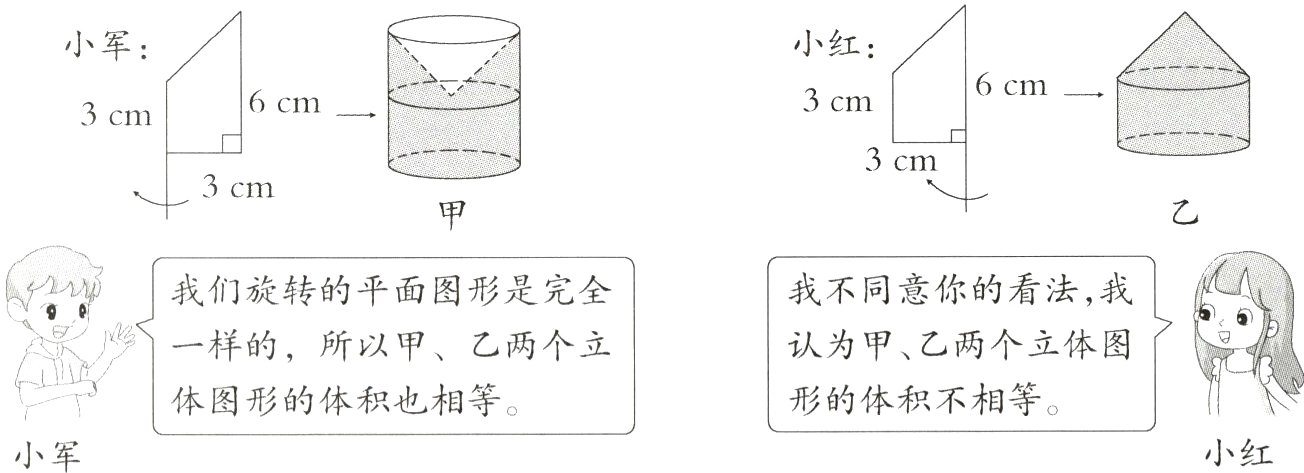
1. ( )的说法对。(3分)
2. 甲、乙两个立体图形的体积比是多少？(7分)

答案： 1. 小红
2. 甲：π×3²×6 - $\frac{1}{3}$×π×3²×(6 - 3)=45π(cm³)
乙：π×3²×3 + $\frac{1}{3}$×π×3²×(6 - 3)=36π(cm³)
45π : 36π = 5 : 4
答：甲、乙两个立体图形的体积比是5 : 4。