《2025年假期冲冠黑龙江教育出版社八年级数学》

11. 已知等腰△ABC的底边BC= 8 cm,|AC-BC|= 2 cm,则腰AC的长为______.

答案： 11. 10 cm 或 6 cm

12. 已知三角形的三边长分别为2,a-1,4,则化简|a-3|+|a-7|的结果为______.

答案： 12. 4

13. 如图,在直角△ABC中,BC边上有E,D,F三点,BD= CD,∠BAE= ∠DAE,AF⊥BC,垂足为F.
(1)以AD为中线的三角形是______;以AE为角平分线的三角形是______;以AF为高线的钝角三角形有______个;
(2)若∠B= 35°,求∠CAF的度数.

答案： 13. 解：
(1)$\triangle ABC$ $\triangle ABD$ 3
(2)在$Rt\triangle ABC$中，$\angle BAC = 90^{\circ}$，$\angle B = 35^{\circ}$，
$\therefore \angle C = 90^{\circ}-35^{\circ}=55^{\circ}$，
$\because AF\perp BC$，
$\therefore \angle CAF = 90^{\circ}-55^{\circ}=35^{\circ}$。

14. 已知a,b,c分别为△ABC的三边长,且满足a-2c= b-14,a+6= 3c-b.
(1)求c的取值范围;
(2)若△ABC的周长为26,求a,b的值,并判断△ABC的形状.

答案： 14. 解：
(1)$\because a - 2c = b - 14$，$a + 6 = 3c - b$，
$\therefore a - b = 2c - 14$，$a + b = 3c - 6$，
则$\left\{\begin{array}{l}|2c - 14|\lt c,\\ 3c - 6\gt c,\end{array}\right.$
解$|2c - 14|\lt c$分两种情况：$2c - 14\lt c$或$-(2c - 14)\lt c$，
$\therefore c\lt 14$或$c\gt \frac{14}{3}$，解$3c - 6\gt c$得$c\gt 3$，
$\therefore \frac{14}{3}\lt c\lt 14$。
(2)$\because \triangle ABC$的周长为 24，$a + b = 3c - 6$，
$\therefore 3c - 6 + c = 24$，解得$c = 7.5$，
$\therefore \left\{\begin{array}{l}a - b = 1,\\ a + b = 16.5,\end{array}\right.$解得$\left\{\begin{array}{l}a = 8.75,\\ b = 7.5,\end{array}\right.$
$\therefore b = c\neq a$，$\therefore \triangle ABC$是等腰三角形。

15. 用一条长44 cm的细绳围成一个三角形,已知第一条边长为x cm,第二条边长比第一条边长的3倍少6 cm.
(1)用含x的式子表示第三条边长;
(2)若能围成一个等腰三角形,求这个三角形的三边长;
(3)若第一条边长最短,直接写出x的取值范围.

答案： 15. 解：
(1)$44 - x - (3x - 6) = (50 - 4x)cm$；
(2)当$x = 3x - 6$时，$x = 3$，不合题意舍去；当$x = 50 - 4x$时，$x = 10$，不合题意舍去；当$3x - 6 = 50 - 4x$时，$x = 8$，此时另两边长都为$3× 8 - 6 = 18$，即这个三角形的三边长分别为 8 cm，18 cm，18 cm；
(3)依题意得$\left\{\begin{array}{l}x\gt 0,\\ 3x - 6\gt x,\\ 50 - 4x\gt x,\\ x + 3x - 6\gt 50 - 4x,\\ x + 50 - 4x\gt 3x - 6,\end{array}\right.$
解得$7\lt x\lt 9\frac{1}{3}$。

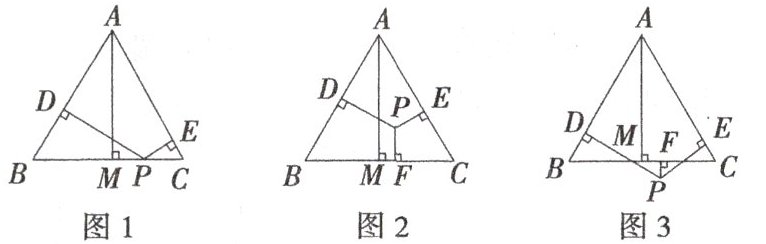
16. 已知等边三角形ABC和点P,设点P到△ABC的三边AB,AC,BC的距离分别为h_{1},h_{2},h_{3},△ABC的高AM为h.若点P在△ABC的边BC上,如图1,此时h_{3}= 0,可得结论h_{1}+h_{2}+h_{3}= h.当点P在△ABC的内部或外部时,如图2,3,上述结论是否仍然成立? 若成立,请给予证明;若不成立,h_{1},h_{2},h_{3}与h之间有怎样的数量关系?请直接写出你的猜想.

答案：
16. 解：当点 P 在$\triangle ABC$的内部时，结论仍然成立。证明如下：
如图，连接 PA，PB，PC，
$\because S_{\triangle ABC} = S_{\triangle PAB} + S_{\triangle PAC} + S_{\triangle PBC}$，
$\therefore \frac{1}{2}BC\cdot h = \frac{1}{2}AB\cdot h_1 + \frac{1}{2}AC\cdot h_2 + \frac{1}{2}BC\cdot h_3$，
$\because \triangle ABC$是等边三角形，
$\therefore AB = AC = BC$，
$\therefore h_1 + h_2 + h_3 = h$。

当点 P 在$\triangle ABC$的外部时，结论不成立，它们之间的关系是$h_1 + h_2 - h_3 = h$。