《2025年假期冲冠黑龙江教育出版社八年级数学》

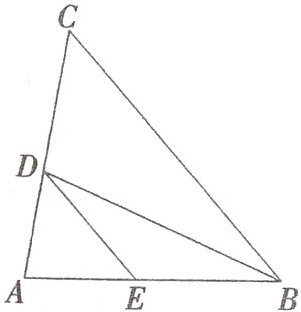
11. 如图,$BD是\triangle ABC$的角平分线,$DE// BC$,交$AB于点E$.
(1)求证：$∠EBD= ∠EDB$.
(2)当$AB= AC$时,请判断$CD与ED$的大小关系,并说明理由.

答案： 解:
(1)证明:
∵BD是△ABC的角平分线,
　
∴∠CBD=∠EBD.
　
∵DE//BC，
∴∠CBD=∠EDB，
∴∠EBD=∠EDB
(2)CD=ED.理由如下
　
∵AB=AC，
∴∠C=∠ABC.
∵DE //BC
　
∴∠ADE=∠C，∠AED=∠ABC，
　
∴∠ADE=∠AED，
　
∴AD=AE，
∴AC−AD=AB−AE，即CD=BE.
　　由
(1)得∠EBD=∠EDB，
∴BE=ED，
∴CD=ED.

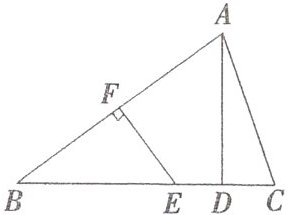
12. 如图,在$\triangle ABC$中,$AB的垂直平分线EF交BC于点E$,交$AB于点F$,$D为线段CE$的中点,$BE= AC$.
(1)求证：$AD⊥BC$；
(2)若$∠BAC= 75^{\circ }$,求$∠B$的度数.

答案：
(1)证明:连接AE.
∵EF垂直平分AB，
∴AE=BE.
　
∵BE=AC，
∴AE=AC.
　
∵D是EC的中点，
∴AD⊥BC;
(2)解:设∠B=x.
∵AE=BE，
　
∴∠BAE=∠B=x.
　
∴∠AEC=2x
　
∵AE=AC，
∴∠C=∠AEC=2x.
　　在△ABC中，3x + 75° = 180°，解得x = 35°，
∴∠B = 35°.

13. 如图,在等边三角形$ABC$中,点$M为AB$边上任意一点,延长$BC至点N$,使$CN= AM$,连接$MN交AC于点P$,$MH⊥AC于点H$.
(1)求证：$MP= NP$；
(2)若$AB= a$,求线段$PH$的长(结果用含$a$的代数式表示).

答案： 解:
(1)证明:如图所示，过点M作MQ//CN.
　
∵△ABC为等边三角形，
　
∴△AMQ为等边三角形，则MQ = AM = CN.
　　又
∵MQ//CN，
∴∠QMP =∠CNP
　　在△MQP与△NCP中
　　$\begin{cases}∠MPQ = ∠NPC\\∠QMP = ∠CNP\\QM = CN\end{cases}$
　
∴△MQP≌△NCP(AAS)，
∴MP = NP;
(2)
∵△AMQ为等边三角形，且MH⊥AC，
∴AH = HQ.
　　又由
(1)得，△MQP≌△NCP，则PQ = PC.
　
∴PH = HQ + PQ = 0.5(AQ + CQ)=0.5AC = 0.5a