《2025年假期冲冠黑龙江教育出版社八年级数学》

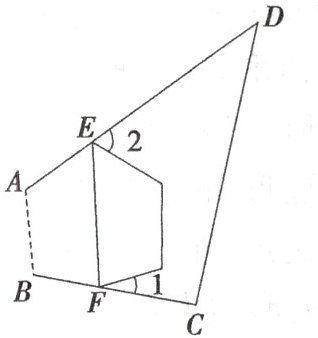
13. 如图,$ E $,$ F $ 分别是四边形 $ A B C D $ 的边 $ A D $,$ B C $ 上的点. 连接 $ E F $,将四边形 $ A B C D $ 沿直线 $ E F $ 折叠. 若点 $ A $,$ B $ 都落在四边形 $ A B C D $ 的内部,记 $ ∠ C + ∠ D = \alpha $,则 $ ∠ 1 + ∠ 2 = $______.

答案： 13. $360^{\circ}-2\alpha$

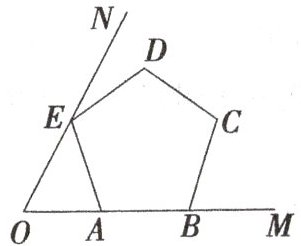
14. 如图所示,已知 $ ∠ M O N = 60 ^ { \circ } $,正五边形 $ A B C D E $ 的顶点 $ A $、$ B $ 在射线 $ O M $ 上,顶点 $ E $ 在射线 $ O N $ 上,则 $ ∠ A E O = $______度.

答案： 14. $48$

15. 一个 $ n $ 边形从一个顶点出发引出的对角线可将其分割成 $ 5 $ 个三角形,则 $ n $ 的值为______.

答案： 15. $7$

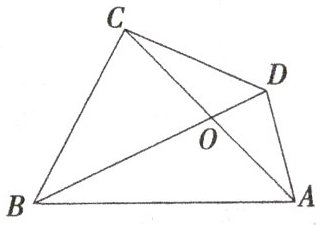
16. 如图,四边形 $ A B C D $ 中,对角线 $ A C $、$ B D $ 交于点 $ O $,$ ∠ A C D = 22 ^ { \circ } $,$ ∠ B D C = 50 ^ { \circ } $,$ ∠ B A C = 2 ∠ A B D $,则 $ ∠ B A C $ 的度数为______.

答案： 16. $48^{\circ}$

17. 一个多边形过顶点剪去一个角后,所得多边形的内角和为 $ 720 ^ { \circ } $,则原多边形的边数是______.

答案： 17. $6$ 或 $7$

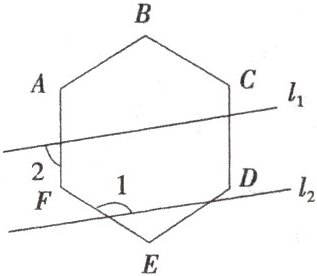
18. 如图,$ l _ { 1 } $ 与 $ l _ { 2 } $ 穿过正六边形 $ A B C D E F $,且 $ l _ { 1 } // l _ { 2 } $,则 $ ∠ 1 - ∠ 2 $ 的度数为______.

答案： 18. $60^{\circ}$

19. 如图,五边形纸片 $ A B C D E $ 内一点 $ P $,连接 $ A P $,$ C P $,得到 $ ∠ 1 + ∠ 2 + ∠ 3 + ∠ 4 = 300 ^ { \circ } $.

(1)求五边形 $ A B C D E $ 的内角和.
(2)在四边形 $ A B C P $ 中,求 $ ∠ A P C $ 的度数.

答案： 19. 解：
(1) $(5 - 2)×180^{\circ}=540^{\circ}$，
$\therefore$ 五边形 $ABCDE$ 的内角和是 $540^{\circ}$。
(2) $\because\angle B+\angle BAP+\angle BCP = 540^{\circ}-(\angle1+\angle2+\angle3+\angle4)$，$\therefore\angle B+\angle BAP+\angle BCP = 540^{\circ}-300^{\circ}=240^{\circ}$，
$\therefore\angle C = 360^{\circ}-240^{\circ}=120^{\circ}$。

20. 如果一个多边形的所有内角都相等,我们称这个多边形为“等角多边形”,现有两个等角多边形,它们的边数之比为 $ 1 : 2 $,且第二个多边形的内角比第一个多边形的内角大 $ 15 ^ { \circ } $,求这两个多边形的边数.

答案： 20. 解：设一个多边形的边数是 $n$，则另一个多边形的边数是 $2n$，则这两个多边形的外角是 $\frac{360^{\circ}}{n}$ 和 $\frac{360^{\circ}}{2n}$，
$\because$ 第二个多边形的内角比第一个多边形的内角大 $15^{\circ}$，
$\therefore\frac{360^{\circ}}{n}-\frac{360^{\circ}}{2n}=15^{\circ}$
解得：$n = 12$，
$\therefore$ 这两个多边形的边数分别为 $12$，$24$。