2025年假期冲冠黑龙江教育出版社八年级数学
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年假期冲冠黑龙江教育出版社八年级数学 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
11. 等腰三角形一腰上的高与另一腰的夹角为25°,求这个三角形各内角的度数。
答案:
11. 解:①当高在△ABC的内部时,如图1.
∵∠ABD = 25°,
∴∠A = 90°−∠ABD = 65°,
∴∠C = ∠ABC = $\frac{1}{2}$×(180°−∠A)=57.5°.

②当高在△ABC的外部时,如图2
∵∠ABD = 25°,
∴∠BAD = 90°−∠ABD = 90°−25° = 65°,
∴∠BAC = 180°−65° = 115°,
∴∠ABC = ∠C = $\frac{1}{2}$×(180°−∠BAC)=32.5°.
综上所述,三角形各内角的度数为65°,57.5°,57.5°,或115°,32.5°,32.5°
11. 解:①当高在△ABC的内部时,如图1.
∵∠ABD = 25°,
∴∠A = 90°−∠ABD = 65°,
∴∠C = ∠ABC = $\frac{1}{2}$×(180°−∠A)=57.5°.

②当高在△ABC的外部时,如图2
∵∠ABD = 25°,
∴∠BAD = 90°−∠ABD = 90°−25° = 65°,
∴∠BAC = 180°−65° = 115°,
∴∠ABC = ∠C = $\frac{1}{2}$×(180°−∠BAC)=32.5°.
综上所述,三角形各内角的度数为65°,57.5°,57.5°,或115°,32.5°,32.5°
12. 很多三角形过它一个顶点的一条直线,可把它分成两个小等腰三角形。由此,请你探究如下几个问题。
(1)如图1,在△ABC中,∠A= 36°,AB= AC,∠1= ∠2,直线BD交AC于D,求证:△ABD与△DBC都为等腰三角形;
(2)请你在图2、图3中,分别过一个你认为合适的三角形顶点画出一条直线,把它们各自分成两个小等腰三角形,并在图中标出所得小等腰三角形两个底角的度数(不证明);
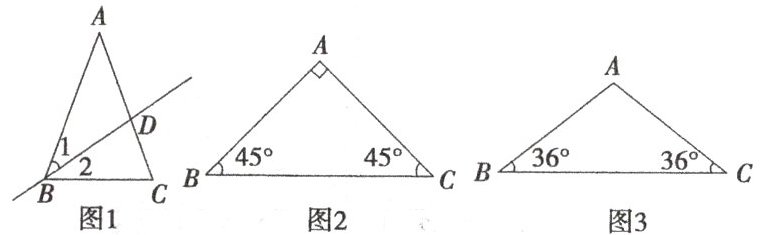
(3)在(1)、(2)中,都是将一个等腰三角形,分成两个小等腰三角形;那么你能把既不是等腰三角形也不是直角三角形的三角形,分成两个小等腰三角形吗?若能,请你设计符合上述条件且6个内角度数均不同的两个三角形,并且分别过一顶点画一直线分成两个小等腰三角形;同时标出所得小等腰三角形两个底角的度数(不证明);若不能,请说明理由。
(1)如图1,在△ABC中,∠A= 36°,AB= AC,∠1= ∠2,直线BD交AC于D,求证:△ABD与△DBC都为等腰三角形;
(2)请你在图2、图3中,分别过一个你认为合适的三角形顶点画出一条直线,把它们各自分成两个小等腰三角形,并在图中标出所得小等腰三角形两个底角的度数(不证明);

(3)在(1)、(2)中,都是将一个等腰三角形,分成两个小等腰三角形;那么你能把既不是等腰三角形也不是直角三角形的三角形,分成两个小等腰三角形吗?若能,请你设计符合上述条件且6个内角度数均不同的两个三角形,并且分别过一顶点画一直线分成两个小等腰三角形;同时标出所得小等腰三角形两个底角的度数(不证明);若不能,请说明理由。
答案:
12. 解:
(1)证明:在△ABC中,
∵AB = AC,
∴∠ABC = ∠C,
∵∠A = 36°,
∴∠ABC = ∠C = $\frac{1}{2}$(180°−∠A)=72°,
∵∠1 = ∠2,
∴∠1 = ∠2 = $\frac{1}{2}$∠ABC = 36°
∴∠3 = ∠1 + ∠A = 72°,
∴∠1 = ∠A,∠3 = ∠C,
∴AD = BD,BD = BC,
∴△ABD与△BDC都是等腰三角形;
(2)如下图所示:


(3)如下图所示:


12. 解:
(1)证明:在△ABC中,
∵AB = AC,
∴∠ABC = ∠C,
∵∠A = 36°,
∴∠ABC = ∠C = $\frac{1}{2}$(180°−∠A)=72°,
∵∠1 = ∠2,
∴∠1 = ∠2 = $\frac{1}{2}$∠ABC = 36°
∴∠3 = ∠1 + ∠A = 72°,
∴∠1 = ∠A,∠3 = ∠C,
∴AD = BD,BD = BC,
∴△ABD与△BDC都是等腰三角形;
(2)如下图所示:


(3)如下图所示:


13. 如图,已知△ABC中,AB= AC= 10cm,BC= 8cm,点D为AB的中点。如果点P在线段BC上以3cm/s的速度由点B向C点运动,同时,点Q在线段CA上由点C向A点运动。
(1)若点Q的运动速度与点P的运动速度相等,经过1秒后,△BPD与△CQP是否全等,请说明理由。
(2)若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△BPD与△CQP全等?
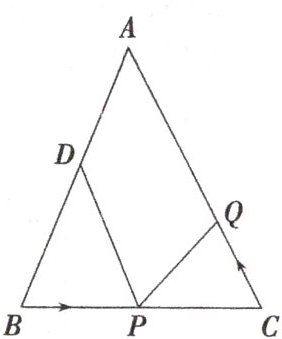
(1)若点Q的运动速度与点P的运动速度相等,经过1秒后,△BPD与△CQP是否全等,请说明理由。
(2)若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△BPD与△CQP全等?

答案:
13. 解:
(1)经过1秒后,PB = 3cm,PC = 5cm,CQ = 3cm,
∵△ABC中,AB = AC,
∴在△BPD和△CQP中
$\begin{cases}BD = PC\\\angle ABC = \angle ACB\\BP = CQ\end{cases}$,
∴△BPD≌△CQP(SAS)
(2)设点Q的运动速度为$x(x≠3)cm/s$,经过$t s$△BPD与△CQP全等;则可知$PB = 3t cm$,$PC = 8 - 3t cm$,$CQ = xt cm$,
∵AB = AC,
∴∠B = ∠C,
根据全等三角形的判定定理SAS可知,有两种情况:①当$BD = PC$,$BP = CQ$时,②当$BD = CQ$,$BP = PC$时,两三角形全等;
①当$BD = PC$且$BP = CQ$时,$8 - 3t = 5$且$3t = xt$,解得$x = 3$,
∵$x≠3$,
∴舍去此情况;
②当$BD = CQ$,$BP = PC$时,$5 = xt$且$3t = 8 - 3t$,解得:$x = \frac{15}{4}$;
故若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为$\frac{15}{4}cm/s$时,能够使△BPD与△CQP全等
(1)经过1秒后,PB = 3cm,PC = 5cm,CQ = 3cm,
∵△ABC中,AB = AC,
∴在△BPD和△CQP中
$\begin{cases}BD = PC\\\angle ABC = \angle ACB\\BP = CQ\end{cases}$,
∴△BPD≌△CQP(SAS)
(2)设点Q的运动速度为$x(x≠3)cm/s$,经过$t s$△BPD与△CQP全等;则可知$PB = 3t cm$,$PC = 8 - 3t cm$,$CQ = xt cm$,
∵AB = AC,
∴∠B = ∠C,
根据全等三角形的判定定理SAS可知,有两种情况:①当$BD = PC$,$BP = CQ$时,②当$BD = CQ$,$BP = PC$时,两三角形全等;
①当$BD = PC$且$BP = CQ$时,$8 - 3t = 5$且$3t = xt$,解得$x = 3$,
∵$x≠3$,
∴舍去此情况;
②当$BD = CQ$,$BP = PC$时,$5 = xt$且$3t = 8 - 3t$,解得:$x = \frac{15}{4}$;
故若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为$\frac{15}{4}cm/s$时,能够使△BPD与△CQP全等
查看更多完整答案,请扫码查看


