2025年假期冲冠黑龙江教育出版社八年级数学
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年假期冲冠黑龙江教育出版社八年级数学 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
1. 在“三角尺拼角”的实验中,小明同学把一副三角尺按如图所示的方式放置,则$∠1$的度数是( )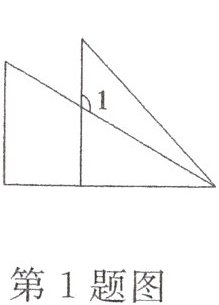
A.$150^{\circ}$
B.$135^{\circ}$
C.$120^{\circ}$
D.$105^{\circ}$

A.$150^{\circ}$
B.$135^{\circ}$
C.$120^{\circ}$
D.$105^{\circ}$
答案:
C
2. 如图,将分别含有$30^{\circ}$、$45^{\circ}$角的一副三角尺重叠,使直角顶点重合,若两直角重叠形成的角为$55^{\circ}$,则图中$∠α$的度数为( )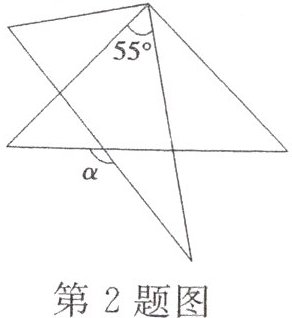
A.$130^{\circ}$
B.$125^{\circ}$
C.$120^{\circ}$
D.$115^{\circ}$

A.$130^{\circ}$
B.$125^{\circ}$
C.$120^{\circ}$
D.$115^{\circ}$
答案:
A
3. 探究与发现:
如图①,有一块直角三角板$DEF放置在△ABC$上,三角板$DEF的两条直角边DE$、$DF恰好分别经过点B$、$C$. 请写出$∠BDC与∠A+∠ABD+∠ACD$之间的数量关系,并说明理由.
应用:
某零件图纸如图②所示,要求$∠A= 90^{\circ}$,$∠B= 32^{\circ}$,$∠C= 21^{\circ}$,当检验员量得$∠BDC= 145^{\circ}$,就断定这个零件不合格,你能利用上述结论说出其中的道理吗?
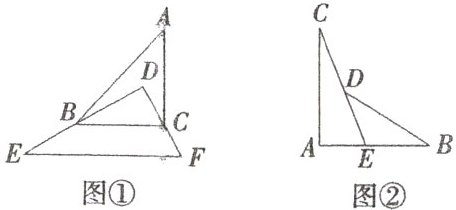
如图①,有一块直角三角板$DEF放置在△ABC$上,三角板$DEF的两条直角边DE$、$DF恰好分别经过点B$、$C$. 请写出$∠BDC与∠A+∠ABD+∠ACD$之间的数量关系,并说明理由.
应用:
某零件图纸如图②所示,要求$∠A= 90^{\circ}$,$∠B= 32^{\circ}$,$∠C= 21^{\circ}$,当检验员量得$∠BDC= 145^{\circ}$,就断定这个零件不合格,你能利用上述结论说出其中的道理吗?

答案:
解:探究与发现:$\angle BDC=\angle A+\angle ABD+\angle ACD$. 理由如下:$\because \angle BDC+\angle DBC+\angle DCB=180^{\circ },\angle A+\angle ABD+\angle ACB=\angle A+\angle ABD+\angle ACD+\angle DBC+\angle DCB=180^{\circ },\therefore \angle BDC=\angle A+\angle ABD+\angle ACD$.
应用:连接 BC,由上述结论得$\angle BDC=\angle A+\angle ABD+\angle ACD=143^{\circ }$. 又
∵由检验员量得$∠BDC=145^{\circ }≠143^{\circ },$
∴这个零件不合格.
应用:连接 BC,由上述结论得$\angle BDC=\angle A+\angle ABD+\angle ACD=143^{\circ }$. 又
∵由检验员量得$∠BDC=145^{\circ }≠143^{\circ },$
∴这个零件不合格.
4. 如图,直线$AB// CD$,如果$∠EFB= 31^{\circ}$,$∠END= 70^{\circ}$,那么$∠E$的度数是( )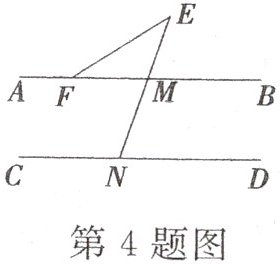
A.$31^{\circ}$
B.$40^{\circ}$
C.$39^{\circ}$
D.$70^{\circ}$

A.$31^{\circ}$
B.$40^{\circ}$
C.$39^{\circ}$
D.$70^{\circ}$
答案:
C
5. 如图,$AB// CD$,直线$PQ分别交AB$,$CD于点F$,$E$,$EG是∠DEF$的平分线,交$AB于点G$. 若$∠PFA= 40^{\circ}$,则$∠EGB$等于( )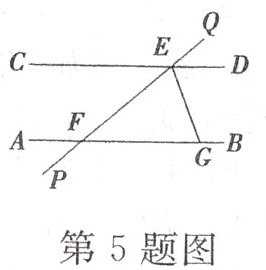
A.$80^{\circ}$
B.$100^{\circ}$
C.$110^{\circ}$
D.$120^{\circ}$

A.$80^{\circ}$
B.$100^{\circ}$
C.$110^{\circ}$
D.$120^{\circ}$
答案:
C
6. 如图,在$△ABC$中,$∠A= 50^{\circ}$,点$M在AB$上,过点$M作MN// BC$,交$AC于点N$,$D是N$上一点,连接$DM$并延长,交$CB的延长线于点E$.
(1)若$∠ABE= 110^{\circ}$,$∠MDN= 70^{\circ}$,求$∠GEF$的度数;
(2)求证:$∠DEG-∠DNM= ∠A+∠EMB$.
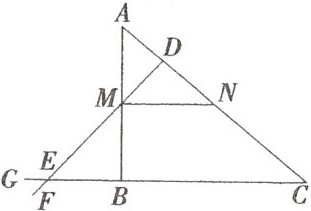
(1)若$∠ABE= 110^{\circ}$,$∠MDN= 70^{\circ}$,求$∠GEF$的度数;
(2)求证:$∠DEG-∠DNM= ∠A+∠EMB$.

答案:
解:
(1)解:$\because \angle ABE=110^{\circ },\angle A=50^{\circ },$$\therefore \angle C=\angle ABE-\angle A=60^{\circ }.\because MN// BC,$$\therefore \angle DMN=\angle MEB,\angle DNM=\angle C=60^{\circ }.\because \angle MDN=70^{\circ },\therefore \angle DMN=180^{\circ }-\angle MDN-\angle DNM=50^{\circ }.\therefore \angle MEB=\angle DMN=50^{\circ }.\therefore \angle GEF=\angle MEB=50^{\circ }.$
(2)证明:$\because \angle DEG=\angle MDN+\angle C,\angle MDN=\angle A+\angle AMD,\therefore \angle DEG=\angle A+\angle AMD+\angle C.\because MN// BC,$$\therefore \angle DNM=\angle C.\because \angle BME=\angle AMD,$$\therefore \angle DEG-\angle DNM=\angle A+\angle EMB.$
(1)解:$\because \angle ABE=110^{\circ },\angle A=50^{\circ },$$\therefore \angle C=\angle ABE-\angle A=60^{\circ }.\because MN// BC,$$\therefore \angle DMN=\angle MEB,\angle DNM=\angle C=60^{\circ }.\because \angle MDN=70^{\circ },\therefore \angle DMN=180^{\circ }-\angle MDN-\angle DNM=50^{\circ }.\therefore \angle MEB=\angle DMN=50^{\circ }.\therefore \angle GEF=\angle MEB=50^{\circ }.$
(2)证明:$\because \angle DEG=\angle MDN+\angle C,\angle MDN=\angle A+\angle AMD,\therefore \angle DEG=\angle A+\angle AMD+\angle C.\because MN// BC,$$\therefore \angle DNM=\angle C.\because \angle BME=\angle AMD,$$\therefore \angle DEG-\angle DNM=\angle A+\angle EMB.$
查看更多完整答案,请扫码查看


