《2025年假期冲冠黑龙江教育出版社八年级数学》

5.如图,△ABC是等边三角形,点D在AC上,点E在BC的延长线上,且BD= DE.
变式题组
(1)若点D是AC的中点,如图①所示,求证:AD= CE;
(2)若点D不是AC的中点,如图②所示,试判断AD与CE的数量关系,并证明你的结论;
(3)若点D在线段AC的延长线上,(2)中的结论是否仍成立?如果成立,给予证明;如果不成立,请说明理由.

答案：
解：
(1) 证明：$\because \triangle ABC$是等边三角形，$\therefore \angle ABC=\angle ACB = 60^{\circ}$，$AB = AC = BC$，$\because D$为$AC$的中点，$\therefore \angle DBC = 30^{\circ}$，$AD = DC$，$\because BD = DE$，$\therefore \angle E=\angle DBC = 30^{\circ}$，$\because \angle ACB=\angle E+\angle CDE$，$\therefore \angle CDE = 30^{\circ}=\angle E$，$\therefore CD = CE$，$\because AD = DC$，$\therefore AD = CE$.
(2)$AD = CE$. 证明如下：过点$D$作$DF// BC$，交$AB$于点$F$，则$\angle ADF=\angle ACB = 60^{\circ}$，$\because \angle A = 60^{\circ}$，$\therefore \triangle AFD$是等边三角形，$\therefore AD = DF = AF$，$\angle AFD = 60^{\circ}$，$\therefore \angle BFD=\angle DCE = 180^{\circ}-60^{\circ}=120^{\circ}$，$\because BD = DE$，$\therefore \angle DBE=\angle E$，$\because DF// BC$，$\therefore \angle FDB=\angle DBE=\angle E$. 在$\triangle BFD$和$\triangle DCE$中，$\left\{\begin{array}{l} \angle FDB=\angle E,\\ \angle BFD=\angle DCE,\\ BD=DE,\end{array}\right.$ $\therefore \triangle BFD≌\triangle DCE$，$\therefore CE = DF = AD$，即$AD = CE$.
(3)
(2)中的结论仍成立. 证明如下：如图，过点$D$作$DP// BC$，交$AB$的延长线于点$P$，$\because \triangle ABC$是等边三角形，$\therefore \triangle APD$也是等边三角形，$\therefore AP = PD = AD$，$\angle APD=\angle ABC=\angle ACB=\angle PDC = 60^{\circ}$，$\therefore \angle DCE = 60^{\circ}$，$\because DB = DE$，
$\therefore \angle DBC=\angle DEC$，$\because DP// BC$，$\therefore \angle PDB=\angle CBD$，$\therefore \angle PDB=\angle DEC$. 在$\triangle BPD$和$\triangle DCE$中，$\left\{\begin{array}{l} \angle PDB=\angle DEC,\\ \angle P=\angle DCE = 60^{\circ},\\ DB=DE,\end{array}\right.$ $\therefore \triangle BPD≌\triangle DCE$，$\therefore PD = CE$，$\therefore AD = CE$.

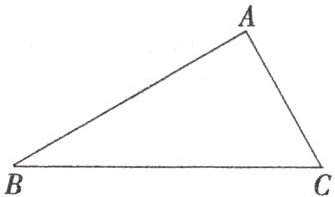
6.如图,在△ABC中,已知∠ACB= 2∠B,BC= 2AC,求证:∠A= 90°.

答案： 证明：过点$C$作$CD$平分$\angle ACB$交$AB$于点$D$，过点$D$作$DE\perp BC$于点$E$，则$\angle ACB = 2\angle DCE$。
$\because \angle ACB = 2\angle B$，
$\therefore \angle DCE = \angle B$，
$\therefore BD = CD$。
$\because DE\perp BC$，
$\therefore BC = 2CE$。
$\because BC = 2AC$，
$\therefore AC = EC$。
在$\triangle ACD$和$\triangle ECD$中，
$\left\{\begin{array}{l} AC = EC \\ \angle ACD = \angle ECD \\ CD = CD \end{array}\right.$，
$\therefore \triangle ACD≌\triangle ECD(SAS)$，
$\therefore \angle A = \angle DEC = 90^{\circ}$。